
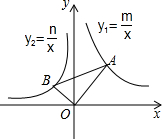
 如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )
如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=$\frac{m}{x}$的图象经过点A,反比例函数y2=$\frac{n}{x}$的图象经过点B,则下列关于m,n的关系正确的是( )| A. | m=$\frac{\sqrt{3}}{3}$n | B. | m=-$\sqrt{3}$n | C. | m=-$\frac{\sqrt{3}}{3}$n | D. | m=-3n |
分析 过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,设点B坐标为(a,$\frac{n}{a}$),点A的坐标为(b,$\frac{m}{b}$),证明△BOE∽△OAF,利用对应边成比例可求出m、n的关系.
解答 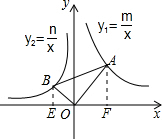 解:过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,
解:过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,
∵∠OAB=30°,
∴OA=$\sqrt{3}$OB,
设点B坐标为(a,$\frac{n}{a}$),点A的坐标为(b,$\frac{m}{b}$),
则OE=-a,BE=$\frac{n}{a}$,OF=b,AF=$\frac{m}{b}$,
∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°,
∴∠OBE=∠AOF,
又∵∠BEO=∠OFA=90°,
∴△BOE∽△OAF,
∴$\frac{OE}{AF}$=$\frac{BE}{OF}$=$\frac{OB}{OA}$,即$\frac{-a}{\frac{m}{b}}$=$\frac{n}{\frac{a}{b}}$=$\frac{1}{\sqrt{3}}$,
解得:m=-$\sqrt{3}$ab,n=$\frac{ab}{\sqrt{3}}$,
故可得:m=-3n.
故选D.
点评 本题考查了反比例函数的综合,解答本题的关键是结合解析式设出点A、B的坐标,得出OE、BE、OF、AF的长度表达式,利用相似三角形的性质建立m、n之间的关系式,难度较大.


科目:初中数学 来源: 题型:选择题
| A. | 31.63% | B. | 46.27% | C. | 53.73% | D. | 68.37% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
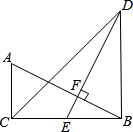 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间,线段最短 | B. | 两点确定一条直线 | ||
| C. | 线段的中点定义 | D. | 直线可以向两边延长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )
如图,OA是北偏东30°方向的一条射线,若∠AOB=90°,则OB的方向角是( )| A. | 北偏西30° | B. | 北偏西60° | C. | 东偏北30° | D. | 东偏北60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
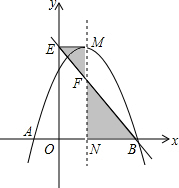 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过抛物线的顶点M作ME⊥y轴于点E,连接BE交MN于点F,已知点A的坐标为(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com