
【题目】如图①,已知OC是∠AOB内部的一条射线,M、N分别为OA、OB上的点,线段OM、ON同时开始旋转,线段OM以30度/秒绕点O逆时针旋转,线段ON以10度/秒的速度绕点O顺时针旋转,当OM旋转到与OB重合时,线段OM、ON都停止旋转.设OM的旋转时间为t秒.

(1)若∠AOB=140°,当t=2秒时,∠MON= ,当t=4秒时,∠MON= ;
(2)如图②,若∠AOB=140°,OC是∠AOB的平分线,求t为何值时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)如图③,若OM、ON分别在∠AOC、∠COB内部旋转时,总有∠COM=3∠CON,请直接写出![]() 的值.
的值.
【答案】(1)60°,20°;(2)t=![]() 或2或
或2或![]() 时;(3)
时;(3)![]() =
=![]() .
.
【解析】
(1)当t=2秒时,线段OM与ON未相遇,根据∠MON=∠AOB-∠AOM-∠BON计算即可;当t=4时,线段OM与ON已相遇过,根据∠MON=∠BON-(∠AOB-∠AOM)计算即可;
(2)分两种情况讨论,列出方程可求解;
(3)由∠COM=3∠CON,列出关于∠AOB,∠BOC的等式,即可求解.
(1)当t=2s时,∠MON=140°﹣10°×2﹣30°×2=60°,如图,
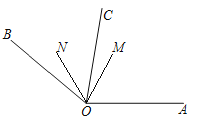
当t=4s时,∠MON=4×10°-(140°-4×30°)=20°,如图,
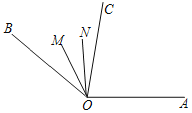
故答案为:60°,20°;
(2)若∠COM=2∠BON时,|30°t﹣70°|=2×10°×t,
∴t=![]() 或7(不合题意舍去)
或7(不合题意舍去)
当∠BON=2∠COM时,2|30°t﹣70°|=10°×t,
∴t=2或![]() ,
,
综上所述当t=![]() 或2或
或2或![]() 时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
时,两个角∠NOB与∠COM中的其中一个角是另一个角的2倍.
(3)∵∠COM=3∠CON,
∴∠AOB﹣∠BOC﹣30°×t=3(∠BOC﹣10°×t),
∴∠AOB=4∠BOC,
∴![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.

(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三点在一条直线上,根据图形填空:
(1)AC= + + ;
(2)AB=AC﹣ ;
(3)DB+BC= ﹣AD
(4)若AC=8cm,D是线段AC中点,B是线段DC中点,求线段AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2),那么,2019的对应点的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们把多元方程(组)的正整数解叫做这个方程(组)的“好解”例如:![]() 就是方程3x+y=11的一组“好解”;
就是方程3x+y=11的一组“好解”;![]() 是方程组
是方程组![]() 的一组“好解”.
的一组“好解”.
(1)请直接写出方程x+2y=7的所有“好解”;
(2)关于x,y,k的方程组![]() 有“好解“吗?若有,请求出对应的“好解”;若没有,请说明理由;
有“好解“吗?若有,请求出对应的“好解”;若没有,请说明理由;
(3)已知x,y为方程33x+23y=2019的“好解”,且x+y=m,求所有m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com