Question

5．如图，△ABC与△DEC均为等腰直角三角形，∠ACB=∠DCE=90°，连接BE，将BE绕点B顺时针旋转90°，得BF，连接AD，BD，AF
（1）如图①，D、E分别在AC，BC边上，求证：四边形ADBF为平行四边形；
（2）△DEC绕点C逆时针旋转，其它条件不变，如图②，（1）的结论是否成立？说明理由．
（3）在图①中，将△DEC绕点C逆时针旋转一周，其它条件不变，问：旋转角为多少度时．四边形ADBF为菱形？直接写出旋转角的度数．

Answer 1

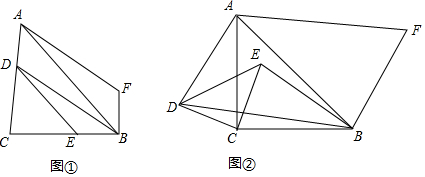
分析 （1）先根据△ABC与△DEC均为等腰直角三角形，以及旋转的性质，得出AD=BF，AD∥BF，进而得到四边形ADBF为平行四边形；
（2）先延长BE交AD于G，交AC于O，根据△ABC与△DEC均为等腰直角三角形，判定△ACD≌△BCE（SAS），得出AD=BE，∠CAD=∠CBE，再根据“8字形”得出∠AGE=90°，判定AD∥BF，即可得出四边形ADBF为平行四边形；
（3）分两种情况讨论：当旋转角∠BCE=135°时，当旋转角为315°时，分别判定△ACD≌△BCD，得到AD=BD，再根据四边形ADBF为平行四边形，得出四边形ADBF为菱形．

解答 解：（1）如图1，∵△ABC与△DEC均为等腰直角三角形，
∴AC-DC=BC-EC，
∴AD=BE，
∵将BE绕点B顺时针旋转90°得BF，
∴BE=BF，
∴AD=BF，
又∵∠ACB=90°，∠CBF=90°，
∴∠C+∠CBF=180°，
∴AD∥BF，
∴四边形ADBF为平行四边形；

（2）如图2，（1）中的结论仍成立．
理由：延长BE交AD于G，交AC于O，
∵△ABC与△DEC均为等腰直角三角形，∠ACB=∠DCE=90°，
∴DC=EC，AC=BC，∠ACD=∠BCE，
∴△ACD≌△BCE（SAS），
∴AD=BE，∠CAD=∠CBE，
又∵BE=BF，∠ACB=90°，∠AOG=∠BOC，
∴AD=BF，∠AGE=90°，
∠AGB+∠EBF=180°，
∴AD∥BF，
∴四边形ADBF为平行四边形；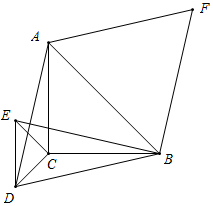

（3）旋转角为135°或315°时，四边形ADBF为菱形．
理由：如图所示，当旋转角∠BCE=135°时，∠ACE=45°，此时∠BCD=135°，
∴∠ACD=∠BCD，
又∵AC=BC，
∴△ACD≌△BCD（SAS），
∴AD=BD，
又∵四边形ADBF为平行四边形，
∴四边形ADBF为菱形；
如图所示，当旋转角为315°时，∠BCE=45°，此时∠BCD=45°，
∵∠ACB=90°，
∴∠ACD=∠BCD，
又∵AC=BC，
∴△ACD≌△BCD（SAS），
∴AD=BD，
又∵四边形ADBF为平行四边形，
∴四边形ADBF为菱形．

点评 本题以旋转为背景，主要考查了四边形的综合应用，解决问题时需要运用全等三角形的判定与性质、等腰直角三角形的性质、旋转的性质以及平行四边形的判定和菱形的判定．解决问题的关键是作辅助线构造“8字形”．解题时注意：两边及其夹角分别对应相等的两个三角形全等．