
分析 (1)根据题意计算即可;
(2)利润=销售量×单位利润.单位利润为x-40,销售量为500-10(x-50),据此表示利润得关系式,进而得出最大利润;
(3)销售成本不超过10000元,即进货不超过10000÷40=250kg.根据利润表达式求出当利润是8000时的售价,从而计算销售量,与进货量比较得结论.
解答 解:(1)销售量:500-5×10=450(kg);
销售利润:450×(55-40)=450×15=6750(元);
(2)由题意可得:
y=(x-40)[500-10(x-50)]
=-10x2+1400x-40000
=-10(x-70)2+9000,
故当销售单价应定为70时,月销售利润最大,最大利润是9000元;
(3)由于水产品不超过10000÷40=250kg,定价为x元,
则(x-40)[500-10(x-50)]=8000
解得:x1=80,x2=60
当x1=80时,进货500-10(80-50)=200kg<250kg,符合题意,
当x2=60时,进货500-10(60-50)=400kg>250kg,舍去.
答:销售单价应为80元.
点评 本题考查了一元二次方程的应用及根据实际问题列二次函数关系式.关键是设售价,分别表示每件利润和销售量,根据求利润的公式列出关系式.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
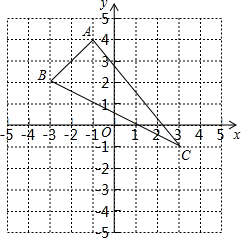 如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).
如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a0=0 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a-2=$\frac{1}{{a}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| a | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.2 | 2 | 20 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com