
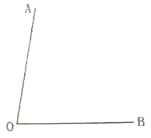
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°,OD是OB的反向延长线.

(1)若∠AOC=∠AOB,求OC的方向.
(2)在(1)问的条件下,作∠AOD的角平分线OE,求∠COE的度数.
【答案】(1)OC的方向是北偏东70°;(2)作∠AOD的角平分线OE,见解析,∠COE=7.5°.
【解析】
(1)由题意先根据OB的方向是西偏北50°求出∠BOF的度数,进而求出∠FOC的度数即可;
(2)根据题意求出∠AOE的度数,再根据角平分线的定义求出∠AOC的度数,然后根据角的和差关系计算即可.
解:(1)∵OB的方向是西偏北50°,
∴∠BOF=90°﹣50°=40°,
∴∠AOB=40°+15°=55°,
∵∠AOC=∠AOB,
∴∠AOC=55°,
∴∠FOC=∠AOF+∠AOC=15°+55°=70°,
∴OC的方向是北偏东70°;
(2)由题意可知∠AOD=90°﹣15°+50°=125°,
作∠AOD的角平分线OE如下图:

∵OE是∠AOD的角平分线,
∴![]() ,
,
∴∠COE=∠AOE﹣∠AOC=62.5°﹣55°=7.5°.


科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是过点
是过点![]() 的一条射线,
的一条射线,![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() .请回答下列问题:
.请回答下列问题:
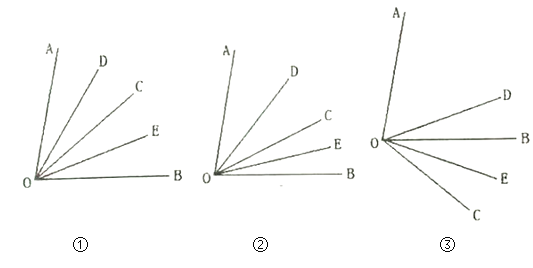
(1)如图①,如果![]() 是
是![]() 的平分线,求
的平分线,求![]() 的度数是多少?
的度数是多少?
(2)如图②,如果![]() 是
是![]() 内部的任意一条射线,
内部的任意一条射线,![]() 的度数有变化吗?为什么?
的度数有变化吗?为什么?
(3)如图③,如果![]() 是
是![]() 外部的任意一条射线,
外部的任意一条射线,![]() 的度数能求出吗?如果能求出,请写出过程;如果不能求出,请简要说明理由.
的度数能求出吗?如果能求出,请写出过程;如果不能求出,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y+1与x+2成正比例,且当x=4时,y=-4.
(1)求y关于x的函数关系式;
(2)若点(a,2)和(2,b)均在(1)中函数图像上,求a、b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面由※组成的图案和算式,解答问题:

![]()
![]()
![]()
![]()
(1)请猜想![]() ____= ______;
____= ______;
(2)请猜想![]() _________;
_________;
(3)请用上述规律计算:![]() 的值;
的值;
(4)请用上述规律计算: ![]() ______(直接写答案).
______(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OC是∠AOB内部的一条射线,M,N分别为OA,OC上的点,线段OM,ON同时分别以30°/s,10°/s的速度绕点O逆时针旋转,设旋转时间为t秒.
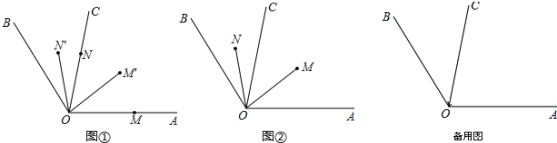
(1)如图①,若∠AOB=120°,当OM、ON逆时针旋转到OM′、ON′处,
①若OM,ON旋转时间t为2时,则∠BON′+∠COM′= °;
②若OM′平分∠AOC,ON′平分∠BOC,求∠M′ON′的值;
(2)如图②,若∠AOB=4∠BOC,OM,ON分别在∠AOC,∠BOC内部旋转时,请猜想∠COM与∠BON的数量关系,并说明理由.
(3)若∠AOC=80°,OM,ON在旋转的过程中,当∠MON=20°,t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.
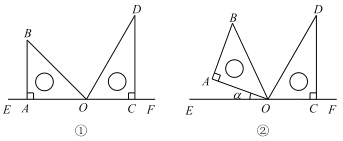
①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
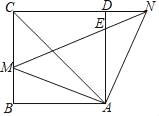
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造美丽校园,小明、小红为校园内的一块空地分别提供了如图甲、乙的设计方案,其中阴影部分都用于绿化,图甲空白区域修建一座雕像,图乙空白区域修建石子小路.已知S甲表示图甲中绿化的面积S乙表示图乙中绿化的面积.
(1)S甲= (用含a,b的代数式表示);
(2)设k=![]() ,
,
①请用含a,b的代数式表示k并化简;
②当2S甲﹣S乙=![]() a2时,求k的值.
a2时,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com