
分析 已知条件中的几个式子有中间变量x,三个式子消去x即可得到:a-b=-2,a-c=-4,b-c=-2,用这三个式子表示出已知的式子,即可求值.
解答 解:∵a=$\frac{1}{20}$x+18,b=$\frac{1}{20}$x+20,c=$\frac{1}{20}$x+22,
∴a-b=-2,a-c=-4,b-c=-2,
∴a2+b2+c2-ab-bc-ac
=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2bc-2ac)
=$\frac{1}{2}$[(a2-2ab+b2)+(a2-2ac+c2)+(b2-2bc+c2)]
=$\frac{1}{2}$[(a-b)2+(a-c)2+(b-c)2]
=$\frac{1}{2}$×(4+16+4)
=12.
故答案为12.
点评 此题主要考查了因式分解的应用,根据题意正确的利用完全平方公式分解因式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,AC与BD交于O点,AB∥DC,AB=DC.
如图,AC与BD交于O点,AB∥DC,AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
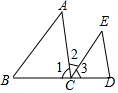 如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.
如图,点C在BD上,请分别根据已知条件进行推理,并在括号内注明推理根据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
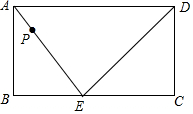 如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.
如图,在矩形ABCD中,点E在BC边上,动点P以2厘米/秒的速度从点A出发,沿△AED的边按照A→E→D→A的顺序运动一周.设点P从A出发经x(x>0)秒后,△ABP的面积是y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com