
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,下面结论: ①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④PQ∥AC.
其中结论正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:∵△ABD、△BCE为等边三角形, ∴AB=DB,∠ABD=∠CBE=60°,BE=BC,
∴∠ABE=∠DBC,∠PBQ=60°,
在△ABE和△DBC中,
∵  ,
,
∴△ABE≌△DBC(SAS),
∴①正确;
∵△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,
∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,
∴②正确;
在△ABP和△DBQ中,
∵  ,
,
∴△ABP≌△DBQ(ASA),
∴BP=BQ,
∴△BPQ为等边三角形,
∴③正确;
∵BP=BQ,∠PBQ=60°,
∴△BPQ是等边三角形,
∴∠PQB=60°,
∴∠PQB=∠QBC,
∴PQ∥AC,
故④正确.
故选D.
①由等边三角形的性质得出AB=DB,∠ABD=∠CBE=60°,BE=BC,得出∠ABE=∠DBC,由SAS即可证出△ABE≌△DBC;
②由△ABE≌△DBC,得出∠BAE=∠BDC,根据三角形外角的性质得出∠DMA=60°;
③由ASA证明△ABP≌△DBQ,得出对应边相等BP=BQ,即可得出△BPQ为等边三角形;
④推出△BPQ是等边三角形,得到∠PBQ=60°,根据平行线的性质即可得到PQ∥AC,故④正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如果二次函数的二次项系数为l,则此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标.
(2)探究下列问题:①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位,再向上平移1个单位,求得到的图象对应的函数的特征数.
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). 
(1)上述操作能验证的等式是;(请选择正确的一个)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
C.a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题: ①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )(1﹣
)(1﹣ ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,点A1 , A2 , A3 , A4和C1 , C2 , C3 , C4分别AB和CD的五等分点,点B1 , B2和D1 , D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为( )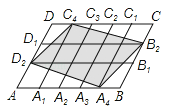
A.2
B.![]()
C.![]()
D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com