练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．阅读理解；我们来定义下面两种数：
    ①平方和数：若一个三位数或三位以上的整数分成左，中，右三个数后满足：中间数=左边数的平方加上右边数的平方，我们就称该整数为平方和数，比如：对于整数251，它的中间数是5，左边数是2，右边数是1，∵22+12=5，∴251为一个平方和数；再比如3254，∵32+42=25，∴3254为一个平方和数；当然.152，4253这两个数肯定也是平方和数；
    ②双倍积数：若一个三位数或三位以上的整数分成左，中，右三个数后满足：中间数=2×左边数×右边数，我们就称该整数为双倍积数；比如：对于整数163，它的中间数为6，左边数为1，右边数为3，∵2×1×3=6，∴163是一个双倍积数；再比如3305，2×3×5=30，∴3305是一个双倍积数；当然，361，5303这两个数也是双倍积数；
    注意：在下列问题中，我们统一用字母a表示一个整数分出来的左边数，用字母b表示一个整数分出来的右边数，请根据上述定义来完成下面问题：
    （1）如果一个三位整数为平方和数，且十位数字是8，则该三位整数是282；如果一个三位整数为双倍积数，且十位数字是4，则该三位整数是142或241；
    （2）若一个整数既是平方和数又是双倍积数，则a，b满足什么数量关系？请说明理由．
    （3）若$\overline{a585b}$为一个平方和数，$\overline{a504b}$为一个双倍积数，求a2-b2．

    分析 （1）可以用试验的办法确定中间数字是8的三位平方和数和中间数字是4的三位双倍积数；
    （2）先用acb表述出该整数，通过它既是平方数又是双倍积数得到：a2+b2=c，c=2ab，从而确定a、b间关系．
    （3）因为a2-b2=（a+b）（a-b），a+b=$\sqrt{{a}^{2}+2ab+{b}^{2}}$，a-b=$\sqrt{{a}^{2}-2ab+{b}^{2}}$由于若$\overline{a585b}$为一个平方和数，$\overline{a504b}$为一个双倍积数根据平方和数和双倍积数的定义，可得到a2+b2，2ab的值，代入即可．

    解答 解：（1）因为22+22=8
    所以一个三位整数为平方和数，且十位数字是8，则该三位整数是282；
    因为2×1×2=4，
    所以一个三位整数为双倍积数，且十位数字是4，则该三位整数是142或241．
    故答案为：282，142或241．
    （2）a，b满足相等关系，即a=b．理由：
    一个整数，字母a表示左边数，字母b表示右边数，该整数的中间部分用字母c表示
    由于该整数是平方数，所以a2+b2=c，
    由于该整数是双倍积数，所以c=2ab，
    所以a2+b2=2ab，即a2+b2-2ab=0
    所以（a-b）2=0，即a=b．
    （3）若$\overline{a585b}$为一个平方和数，则a2+b2=585
    $\overline{a504b}$为一个双倍积数，则2ab=504
    所以a2-b2=（a+b）（a-b）
    =$\sqrt{{a}^{2}+2ab+{b}^{2}}$×$\sqrt{{a}^{2}-2ab+{b}^{2}}$
    =$\sqrt{1089}$×$\sqrt{81}$
    =33×9=297．

    点评 本题考查了完全平方公式、因式分解的相关知识，属于创新类题目．理解平方和数和双倍积数是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．用适当方法解方程
    （1）2x2+1=3x        
    （2）x2-3x-1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解方程：
    （1）3x2+4x+1=0                      
    （2）x2-x-6=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，在平面直角坐标系中，已知B（8，0），C（0，6），P（-3，3），现将一直角三角板EPF的直角顶点放在点P处，EP交y轴于N，FP交x轴于M，把△EPF绕点P旋转：
    （1）如图甲，①求OM+ON的值；②求BM-CN的值；
    （2）如图乙，①求ON-OM的值；②求BM+CN的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，已知∠1+∠2=180°，∠A=∠C，AD平分∠EDB．求证：∠3=∠4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，矩形ABCD中，A在坐标原点，B、D分别在x轴、y轴的正半轴上，且AB=8，AD=6，
    （1）请直接写出其余三个顶点的坐标B（8，0），C（8，6），D（0，6）
    （2）点P从点D向C运动，速度为1个单位/秒，点Q从点B向A运动，速度点P相同，设运动时间为t秒，t为何值时C点在PQ的垂直平分线上，并直接写出此时P、Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．$\sqrt{16}$的平方根为±2；$\sqrt{（1-\sqrt{3}）^{2}}$=$\sqrt{3}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

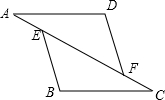    15．如图，点A，B，F，C在同一直线上，AB=FC，DF=EB，DF∥BE．
    （1）试判断AD与CE相等吗？
    （2）AD与CB的位置关系如何？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．为了满足广大市民对新能源汽车的需求，我市某汽车销售公司决定到某汽车制造厂采购A，B两种型号的新能源轿车．若用300万元，则可购进A型轿车10辆，B型轿车15辆；若用320万元，则可购进A型轿车8辆，B型轿车20辆，求A，B两种型号的新能源轿车的单价分别为多少万元？

    查看答案和解析>>

    同步练习册答案