
【题目】为解决“最后一公里”的交通接驳问题,某市投放了大量公租自行车使用,到2014年底,全市已有公租自行车25000辆,租赁点600个,预计到2016年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西南宁市)在南宁市地铁1号线某段工程建设中,甲队单独完成这项工程需要150天,甲队单独施工30天后增加乙队,两队又共同工作了15天,共完成总工程的![]() .
.
(1)求乙队单独完成这项工程需要多少天?
(2)为了加快工程进度,甲、乙两队各自提高工作效率,提高后乙队的工作效率是![]() ,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂。”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少。
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树。他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约_______千米。
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米。小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 于点D.可知:
于点D.可知:![]() 不需要证明
不需要证明![]() ;
;
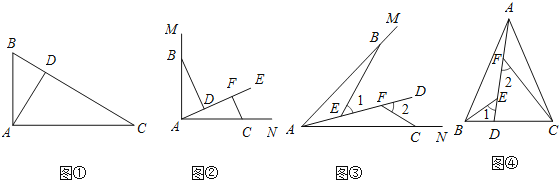
![]() 特例探究:如图
特例探究:如图![]() ,
,![]() ,射线AE在这个角的内部,点B、C在
,射线AE在这个角的内部,点B、C在![]() 的边AM、AN上,且
的边AM、AN上,且![]() ,
,![]() 于点F,
于点F,![]() 于点
于点![]() 证明:
证明:![]() ≌
≌![]() ;
;
![]() 归纳证明:如图
归纳证明:如图![]() ,点B,C在
,点B,C在![]() 的边AM、AN上,点E,F在
的边AM、AN上,点E,F在![]() 内部的射线AD上,
内部的射线AD上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角
的外角![]() 已知
已知![]() ,
,![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 拓展应用:如图
拓展应用:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() 点D在边BC上,
点D在边BC上,![]() ,点E、F在线段AD上,
,点E、F在线段AD上,![]() 若
若![]() 的面积为24,则
的面积为24,则![]() 与
与![]() 的面积之和为______
的面积之和为______![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
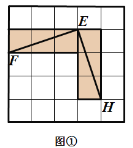
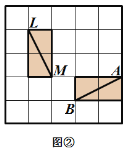
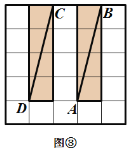
【题目】阅读材料后完成.
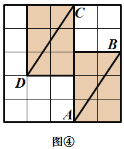
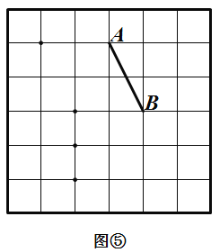
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为![]() 的
的![]() 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知![]() .在图③ 和图④中,可知
.在图③ 和图④中,可知![]() . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的![]() 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段![]() 垂直 的线段(或者直线)
垂直 的线段(或者直线)![]() ,再画出与线段
,再画出与线段![]() 平行的一条线段(或者 直线)
平行的一条线段(或者 直线)![]() . 第二关:在图⑥的
. 第二关:在图⑥的![]() 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知两点A(3,0),B(0,4),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: ;
(2)求证:BM=BN;
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是![]()
![]()
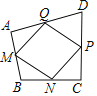
A. 当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B. 当M,N,P,Q是各边中点,且![]() 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形
C. 当M,N、P,Q是各边中点,且![]() 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形
D. 当M,N、P、Q是各边中点,且![]() 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com