
����Ŀ��![]() ��
��![]() ��
��![]() ���ǵ�
���ǵ�![]() ����������գ�Ϊӭ�ӵ�
����������գ�Ϊӭ�ӵ�![]() ����������յĵ�����ijУ�ٰ�������������������ԡ��Ƽ�������Ϊ���⣬������ѡ��һ���Լ���ϲ�����飬Ȼ�������дһ���Ƽ��һƪ�����ĵá��ٰ�һ�����齲����������ί��Բ������ύ���Ƽ�������ĵá��ٰ�Ķ��齲�����д�֣�����ɼ������ٷ��ƣ����ۺϳɼ�������һ��ѡ�ֽ���ô���һ�Ƚ������мס�����λͬѧ�ĸ���ɼ����±���ʾ��
����������յĵ�����ijУ�ٰ�������������������ԡ��Ƽ�������Ϊ���⣬������ѡ��һ���Լ���ϲ�����飬Ȼ�������дһ���Ƽ��һƪ�����ĵá��ٰ�һ�����齲����������ί��Բ������ύ���Ƽ�������ĵá��ٰ�Ķ��齲�����д�֣�����ɼ������ٷ��ƣ����ۺϳɼ�������һ��ѡ�ֽ���ô���һ�Ƚ������мס�����λͬѧ�ĸ���ɼ����±���ʾ��
������ | �Ƽ��� | �����ĵ� | ���齲�� |
�� |
|
|
|
�� |
|
|
|
��1����������ɼ���ƽ������Ϊ����ѡ�ֵ��ۺϳɼ�����ס��Ҷ���˭���п��ܻ�ô���һ�Ƚ�����ͨ������˵�����ɣ�
��2�������Ƽ���������ĵá������齲�����ijɼ���![]() ȷ���ۺϳɼ�����ס��Ҷ���˭���п��ܻ�ô���һ�Ƚ�����ͨ������˵�����ɣ�
ȷ���ۺϳɼ�����ס��Ҷ���˭���п��ܻ�ô���һ�Ƚ�����ͨ������˵�����ɣ�
���𰸡�(1) �����п��ܻ�ô���һ�Ƚ�����2�������п��ܻ�ô���һ�Ƚ�
��������
��1������ƽ�����ļ��㹫ʽ�г���ʽ�����ƽ���������бȽϣ����ɵó��𰸣�
��2�����ݼ�Ȩƽ�����ļ��㹫ʽ�г���ʽ�����м��㼴�ɣ�
�⣺��1�������п��ܻ�ô���һ�Ƚ���
![]() ��ƽ���ɼ�Ϊ
��ƽ���ɼ�Ϊ![]() ���֣�
���֣�
�ҵ�ƽ���ɼ�Ϊ![]() ���֣���
���֣���
![]() ��
��![]() ֪�����п��ܻ�ô���һ�Ƚ���
֪�����п��ܻ�ô���һ�Ƚ���
��2�������п��ܻ�ô���һ�Ƚ���
![]() �ļ�Ȩƽ���ɼ�Ϊ
�ļ�Ȩƽ���ɼ�Ϊ![]() ���֣�
���֣�
�ҵļ�Ȩƽ���ɼ�Ϊ![]() ���֣���
���֣���
![]() ��
��![]() ֪�����п��ܻ�ô���һ�Ƚ���
֪�����п��ܻ�ô���һ�Ƚ���
�ʴ�Ϊ��(1) �����п��ܻ�ô���һ�Ƚ�����2�������п��ܻ�ô���һ�Ƚ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() ��
��![]() �и���4���۶ϣ���
�и���4���۶ϣ���![]() ����
����![]() ����
����![]() ����
����![]() ��
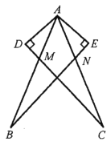
��![]() ���ֽ�4���۶Ϸֱ�ճ�����ĸ�ѧ���ĺ��ϣ�����������Ϸ����������ѧ��վ�ڽ�̨����ߣ���һ��ѧ��վ�ڽ�̨���ұߣ�Ҫ��������ѧ�����ϵIJ����۶���Ϊ���裬��һ��ѧ�����ϵ��۶���Ϊ���ۣ�ʹ֮��Ϊһ�����������Ŀ�������Ϸ�ɽ��м��֣��������е�һ���������֤����
���ֽ�4���۶Ϸֱ�ճ�����ĸ�ѧ���ĺ��ϣ�����������Ϸ����������ѧ��վ�ڽ�̨����ߣ���һ��ѧ��վ�ڽ�̨���ұߣ�Ҫ��������ѧ�����ϵIJ����۶���Ϊ���裬��һ��ѧ�����ϵ��۶���Ϊ���ۣ�ʹ֮��Ϊһ�����������Ŀ�������Ϸ�ɽ��м��֣��������е�һ���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ,�ڵ�������ABCD��,AD��BC,AB=DC����EΪ��BC��һ��,��AE=DC.
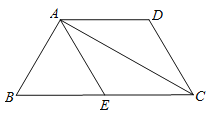
��1����֤:�ı���AECD��ƽ���ı���;
��2������B=2��DCAʱ,��֤�ı���AECD������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+2�������ύ��A��B���㣬��A��x���ϣ���B��y���ϣ�C�������Ϊ��1��0����������y=ax2+bx+c������A��B��C��
��1����������ߵĽ���ʽ��
��2������ͼ��ֱ��д������ʽax2+��b��1��x+c��2�Ľ⼯��
��3����P����������һ���㣬����ֱ��AB�Ϸ�������P��AB�Ĵ��߶Σ�����ΪQ�㣮��PQ=![]() ʱ����P�����꣮
ʱ����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��x����A��B���㣬��y����C�㣬���Щ�2��h����1����1��xB��0�����н��ۢ�abc��0������4a��b����2a+b����0����4a��c��0������OC=OB����a+1����c+1����0����ȷ��Ϊ��������
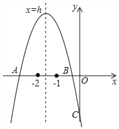
A. �٢ڢۢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��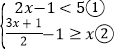
����������գ���ɱ���Ľ��
�������ⲻ��ʽ�٣����� ����
�������ⲻ��ʽ�ڣ����� ����
�������Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������
![]()
������ԭ����ʽ��Ľ⼯Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ĺ�������ʽΪ
�ĺ�������ʽΪ![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ������
������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
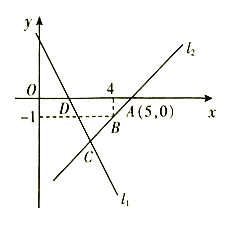
��1����ֱ��![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����![]() �������
�������
��3����ֱ��![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() �����
�����![]() �����
�����![]() ����������ڣ������
����������ڣ������![]() ���ꣻ��������ڣ���˵�����ɣ�
���ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
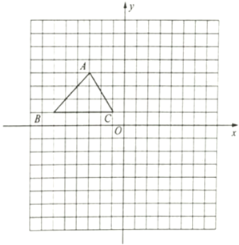
��1������![]() ����ԭ�����ĶԳƵ�
����ԭ�����ĶԳƵ�![]() ������A��B��C�Ķ�Ӧ��ֱ�Ϊ
������A��B��C�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
��2���ڣ�1���Ļ����ϣ���![]() ����ƽ��4����λ���ȣ�����ƽ�ƺ��
����ƽ��4����λ���ȣ�����ƽ�ƺ��![]() ����д��
����д��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() �����ꣻ
�����ꣻ
��3��DΪy����һ�㣬��![]() ����ABΪֱ�DZߵ�ֱ��������.��ֱ��д��D�������.
����ABΪֱ�DZߵ�ֱ��������.��ֱ��д��D�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������εĵ�������������һ���㣬������һ�㣬�ڶ���ÿ�������㣬������ÿ�������㣬�Դ����ƣ�

��1��������
���� |
|
|
|
|
|
�ò��Ӧ�ĵ��� |
|
|
| ________ | ________ |
��2��д����![]() ���Ӧ�ĵ�����
���Ӧ�ĵ�����![]() ����
����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com