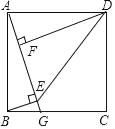
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，四边形ABED的面积为6，求EF的长．
【答案】（1）证明见解析；（2）EF=2．
【解析】试题分析：（1）由∠BAE+∠DAF=90°，∠DAF+∠ADF=90°，推出∠BAE=∠ADF，即可根据AAS证明△ABE≌△DAF；
（2）设EF=x，则AE=DF=x+1，根据四边形ABED的面积为6，列出方程即可解决问题；
试题解析：解：（1）∵四边形ABCD是正方形，∴AB=AD，∵DF⊥AG，BE⊥AG，∴∠BAE+∠DAF=90°，∠DAF+∠ADF=90°，∴∠BAE=∠ADF，在△ABE和△DAF中，∵∠BAE=∠ADF，∠AEB=∠DFA，AB=AD，∴△ABE≌△DAF（AAS）．
（2）设EF=x，则AE=DF=x+1，由题意2×
×（x+1）×1+×x×（x+1）=6，解得x=2或﹣5（舍弃），∴EF=2．
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，已知
中，
，
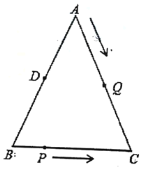
，点D为AB的中点．如果点P在线段BC上以2cm/s的速度由点B向C点运动，同时，点Q在线段AC上由点A向C点以4cm/s的速度运动．
（1）若点P、Q两点分别从B、A两点同时出发，经过2秒后，
与
是否全等？请说明理由；
（2）若点P、Q两点分别从B、A两点同时出发，的周长为16cm，设运动时间为t，问：当t为何值时，是等腰三角形？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知下列命题：①相等的角是对顶角；②互补的角就是平角；③互补的两个角一定是一个锐角，另一个为钝角：④平行于同一条直线的两直线平行；⑤两条平行线被第三条直线所截，同旁内角的角平分线互相垂直．其中，正确命题的个数为（ ）
A.0B.1个C.2个D.3个
查看答案和解析>>
科目：初中数学 来源： 题型：
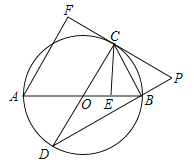
【题目】（2017广东省）如图，AB是⊙O的直径，AB=
，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，AF⊥PC于点F，连接CB．
（1）求证：CB是∠ECP的平分线；
（2）求证：CF=CE；
（3）当
时，求劣弧
的长度（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料，并解决有关问题
我们知道：
|a|＝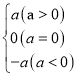
现在我们可以用这一结论来化解含有绝对值的代数式
如化简代数式|x+1|+|x﹣2|时，可令x+1＝0和x﹣2＝0，分别求得x＝﹣1和x＝2（称﹣1，2分别为|x+1|和|x﹣2|的零点值）
在实数范围内，零点值x＝﹣1和x＝2可将全体实数分成不重复且不遗漏的如下三种情况：
（1）x＜﹣1（2）﹣1≤x＜2（3）x≥2
从而化简代数式|x+1|+|x﹣2|，可分以下三种情况
（1）x＜﹣1时，原式＝﹣（x+1）﹣（x﹣2）＝﹣2x+1
（2）﹣1≤x＜2时，原式＝x+1﹣（x﹣2）＝3
（3）x≥2时，原式＝x+1+x﹣2＝2x﹣1
通过以上阅读，请你解决以下问题
（1）化简代数式|x+2|+|x﹣4|
（2）求|x﹣1|﹣4|x+1|的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
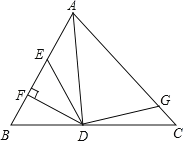
【题目】如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和40，则△EDF的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
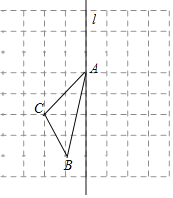
（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；
（2）在直线l上找一点P，使PB′+PC的长最短；
（3）若△ACM是以AC为腰的等腰三角形，点M在小正方形的顶点上．这样的点M共有 个．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
