
 中,
中, ,
, .它的顶点
.它的顶点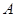 的坐标为
的坐标为 ,顶点
,顶点 的坐标为
的坐标为 ,
, ,点
,点 从点
从点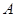 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点 出发,沿
出发,沿 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点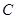 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为 秒.
秒.
 的度数.
的度数. 在
在 上运动时,
上运动时, 的面积
的面积 (平方单位)与时间
(平方单位)与时间 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度. 与时间
与时间 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标. 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿 边运动时,
边运动时,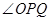 的大小随着时间
的大小随着时间 的增大而增大;沿着
的增大而增大;沿着 边运动时,
边运动时,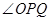 的大小随着时间
的大小随着时间 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使 的点
的点 有几个?请说明理由.
有几个?请说明理由. (2)点
(2)点 的运动速度为2个单位/秒(3)
的运动速度为2个单位/秒(3)
 ,
, (4)有2个,理由见解析
(4)有2个,理由见解析 .························· 2分
.························· 2分 的运动速度为2个单位/秒.····················· 4分
的运动速度为2个单位/秒.····················· 4分 (
( )
) ··························· 6分
··························· 6分 .
. 当
当 时,
时, 有最大值为
有最大值为 ,
, .····························· 9分
.····························· 9分 沿这两边运动时,
沿这两边运动时, 的点
的点 有2个.·········· 11分
有2个.·········· 11分 与点
与点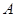 重合时,
重合时, ,
, 运动到与点
运动到与点 重合时,
重合时, 的长是12单位长度,
的长是12单位长度, 交
交 轴于点
轴于点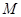 ,作
,作 轴于点
轴于点 ,
, 得:
得: ,
, ,从而
,从而 .
. 在
在 边上运动时,
边上运动时, 的点
的点 有1个.·········· 13分
有1个.·········· 13分 在
在 边上运动时,
边上运动时,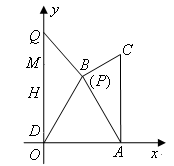
 .
. 轴于
轴于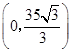 ,
, ,
, ,从而
,从而 的点
的点 也有1个.
也有1个. 沿这两边运动时,
沿这两边运动时, 的点
的点 有2个.··········· 14分
有2个.··········· 14分 ,因此∠BAO=60°
,因此∠BAO=60° ,也就是P到OQ的距离为10-
,也就是P到OQ的距离为10- ,OQ=QD+OD=5a+2.因此(5a+2)×(10-
,OQ=QD+OD=5a+2.因此(5a+2)×(10- )×
)× =30,解得a=1.6,a=2.由于抛物线的解析式为S=(at+2)(10-
=30,解得a=1.6,a=2.由于抛物线的解析式为S=(at+2)(10-  )×
)× ,经化简后可得出对称轴应该是t=
,经化简后可得出对称轴应该是t=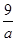 ,当a=1.6时,对称轴t=5.625显然大于5,与给出的抛物线的图形不相符,因此a=2是本题的唯一的解.也就是说P的速度是2单位/秒.
,当a=1.6时,对称轴t=5.625显然大于5,与给出的抛物线的图形不相符,因此a=2是本题的唯一的解.也就是说P的速度是2单位/秒.

科目:初中数学 来源:不详 题型:解答题
 交
交 轴于
轴于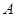 、
、 两点,交
两点,交 轴于点
轴于点 ,已知抛物线的对称轴为
,已知抛物线的对称轴为 ,
, ,
, ,
, 的解析式;
的解析式; ,使点
,使点 到
到 、
、 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由; 轴的一条直线交抛物线于
轴的一条直线交抛物线于 两点,若以
两点,若以 为直径的圆恰好与
为直径的圆恰好与 轴相切,求此圆的半径.
轴相切,求此圆的半径.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与
的图象与 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数
.一个二次函数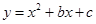 的图象经过点
的图象经过点 .
.
 的坐标,并画出一次函数
的坐标,并画出一次函数 的图象;
的图象;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=2(x+1)2+3 | B.y=2(x-1)2-3 |
| C.y=2(x+1)2-3 | D.y=2(x-1)2+3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 从点
从点 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿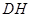 运动到点
运动到点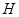 停止,在运动过程中,过点
停止,在运动过程中,过点 作
作 交折线
交折线 于点
于点 ,将纸片沿直线
,将纸片沿直线 折叠,点
折叠,点 、
、 的对应点分别是点
的对应点分别是点 、
、 。设
。设 点运动的时间是
点运动的时间是 秒(
秒( )。
)。 和点
和点 重合时,求运动时间
重合时,求运动时间 的值;
的值; 或四边形
或四边形 与梯形
与梯形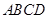 重叠部分面积为
重叠部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应自变量
之间的函数关系式和相应自变量 的取值范围;
的取值范围; ,交线段
,交线段 于点
于点 ,交线段
,交线段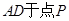 。在直线
。在直线 上存在点
上存在点 ,使
,使 为等腰直角三角形。请求出线段
为等腰直角三角形。请求出线段 的所有可能的长度。
的所有可能的长度。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com