
【题目】如图,点A、B在双曲线y=![]() (x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=
(x<0)上,连接OA、AB,以OA、AB为边作□OABC.若点C恰落在双曲线y=![]() (x>0)上,此时□OABC的面积为__________.
(x>0)上,此时□OABC的面积为__________.

【答案】![]()
【解析】
如图,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,设A(a,﹣![]() ),C(b,
),C(b,![]() ),根据△ABF≌△COE可得B(a+b,﹣
),根据△ABF≌△COE可得B(a+b,﹣![]() ),即(a+b)(﹣
),即(a+b)(﹣![]() )=﹣3,设
)=﹣3,设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,求得
=2,求得![]() =
=![]() ,
,![]() ,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
,然后根据□OABC的面积=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
解:如图,连接AC,过A点作AD⊥x轴于D,过C作CE⊥x轴于E,过B作BF⊥AD于F,
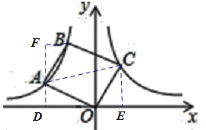
易证△ABF≌△COE,设A(a,﹣![]() ),C(b,
),C(b,![]() ),则OE=BF=b,CE=AF=
),则OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
∵B点在在双曲线y=![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
设![]() =m,则可化方程为3m﹣
=m,则可化方程为3m﹣![]() =2,
=2,
解得m=![]() ,或m=
,或m=![]() (舍去),
(舍去),
∴![]() =
=![]() ,
,![]() ,
,
∴S□OABC=2×S△OAC
=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×∣﹣3∣﹣
×∣﹣3∣﹣![]() ×2]
×2]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=![]() .
.
故答案为:![]() .
.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
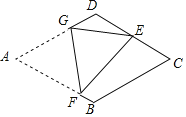
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=20°.将△ABC绕点C按逆时针方向旋转得△A′B′C,且点B在A′B′ 上,CA′ 交AB于点D,则∠BDC的度数为( )
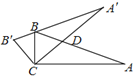
A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=AC,CF垂直直径BD于点E,交边AB于点F.
(1)求证:∠BFC=∠ABC.
(2)若⊙O的半径为5,CF=6,求AF长.
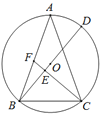
查看答案和解析>>
科目:初中数学 来源: 题型:
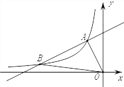
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
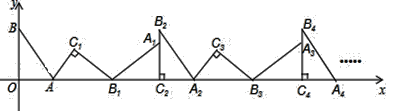
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
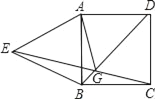
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com