练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，在△ABC中，∠B=40°，∠C=62°，AD是△ABC的高，AE是△ABC的角平分线．求∠EAD的度数．

    分析 首先根据三角形的内角和定理，求出∠BAC的度数是多少；然后根据AE为角平分线，求出∠BAE的度数是多少；最后在Rt△DAC中，求出∠DAC的度数，即可求出∠EAD的度数是多少．

    解答 解：∵∠B=40°，∠C=62°，
    ∴∠BAC=180°-62°-40°=78°，
    ∵AE为∠BAC角平分线，
    ∴∠BAE=78°÷2=39°，
    ∵AD为△ABC的高，
    ∴∠ADB=90°，
    ∴∠DAC=90°-∠C=90°-62°=28°，
    ∴∠EAD=∠EAC-∠DAC=39°-28°=11°，
    即∠EAD的度数是11°．

    点评 此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．此题还考查了三角形的外角的性质和应用，要熟练掌握．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．某农场要建一个长方形的养鸡场，鸡场的一边靠墙，墙长25m，另外三边用木栏围成，木栏长40m．
    （1）若养鸡场面积为200m2，画出示意图并求鸡场靠墙的一边长．
    （2）养鸡场面积能达到250m2吗？如果能，请给出设计方案，如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知二次函数y=x2+bx+c的图象经过点（-2，4）和（1，-2），试确定b，c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．小明与小刚规定了一种新运算△：a△b=（-$\frac{1}{a}$）÷$\frac{b}{2}$，请你帮他们计算-2△5=$\frac{1}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列说法中正确的是（　　）
    A．|a|一定是正数B．-a一定是负数
    C．-（-a）一定是正数D．如果$\frac{|a|}{a}=-1$，那么a＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，已知△ABF≌△DEC，说明AC∥DF成立的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

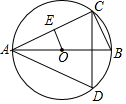    18．如图，已知AB是⊙O的直径，点C，D在⊙O上，且AB=6，∠CAB=30°
    （1）求∠ADC的度数；
    （2）如果OE⊥AC，垂足为E，求OE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知a，b，c为三个不等于0的数，且满足abc＞0，a+b+c＜0，求$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知a与b互为相反数，c与d互为倒数，m的绝对值为4，求$\frac{2}{3}a+\frac{2}{3}b+（cd）^{2013}-\frac{3}{2}$m的值．

    查看答案和解析>>

    同步练习册答案