
分析 求出方程的解,分为两种情况,看看是否符合三角形三边关系定理,求出即可.
解答 解:由方程x2-8x+15=0得:(x-3)(x-5)=0,
∴x-3=0或x-5=0,
解得:x=3或x=5,
当等腰三角形的三边长为9、9、3时,其周长为21;
当等腰三角形的三边长为9、9、5时,其周长为23;
当等腰三角形的三边长为9、3、3时,3+3<9,不符合三角形三边关系定理,舍去;
当等腰三角形的三边长为9、5、5时,其周长为19;
综上,该等腰三角形的周长为19或21或23,
故答案为:19或21或23.
点评 本题考查了解一元二次方程和等腰三角形性质,三角形的三边关系定理的应用,因式分解法求出方程的解是根本,根据等腰三角形的性质分类讨论是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
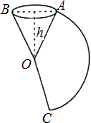 如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).
如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12cm,OA=13cm,则扇形AOC中$\widehat{AC}$的长是10πcm(计算结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
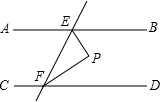 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=44°,则∠EPF=67°.
如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=44°,则∠EPF=67°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com