
 .
.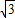 MQ-CN整理即可得解;
MQ-CN整理即可得解; (AD+CB),再根据(1)得到DE的长,根据三角形的中位线平行于第三边并且等于第三边的一半可得PF∥DE,PF=
(AD+CB),再根据(1)得到DE的长,根据三角形的中位线平行于第三边并且等于第三边的一半可得PF∥DE,PF= DE,根据同角的余角相等求出∠QPM=∠FPN,然后求出△PQM和△PFN相似,利用相似三角形对应边成比例列式求出MQ和FN的关系,再表示出CN,整理即可得解.
DE,根据同角的余角相等求出∠QPM=∠FPN,然后求出△PQM和△PFN相似,利用相似三角形对应边成比例列式求出MQ和FN的关系,再表示出CN,整理即可得解.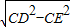 =
=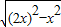 =
=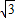 x,
x,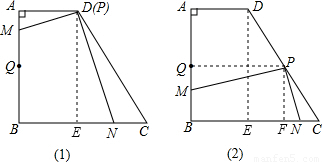
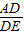 =
=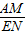 ,
,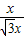 =
=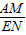 ,
,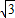 AM,
AM, AB=
AB= DE=
DE=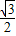 x,
x,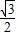 x-AM,
x-AM,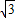 MQ-CN=
MQ-CN=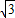 (
(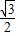 x-AM)-(x-
x-AM)-(x-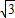 AM)=
AM)= x-
x-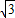 AM-x+
AM-x+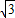 AM=
AM= x,
x, x=
x= BC,
BC,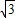 MQ-CN=
MQ-CN= BC;
BC; (AD+CB)=
(AD+CB)= (x+2x)=
(x+2x)= x,
x,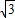 x,
x, DE=
DE= x,CF=
x,CF= CE=
CE= x,
x,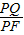 =
=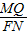 ,
,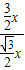 =
=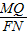 ,
,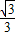 MQ,
MQ, x-
x-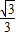 MQ,
MQ, x=
x= BC,
BC,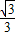 MQ+CN=
MQ+CN= BC.
BC.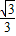 MQ+CN=
MQ+CN= BC.
BC.

科目:初中数学 来源: 题型:
| 4 | 3 |
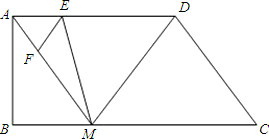 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com