

���� ��1������ȫ�������ε����ʺ���������λ�߶���֤�����ɣ�
��2���������������ε��ж������ʵó�MQ��PN���ٸ��ݾ��ε��ж���ɣ�
��3��ֱ��д��ͼ�ε���״���ɣ�
��� ��1��֤�����ߡ�ABC���AEF����ֱ��AD�Գƣ���ͼ1��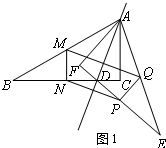
���ABC�ա�AEF��
��AC=AF��
�ߵ�M��N��P��Q�ֱ���AB��BC��EF��EA���е㣬
��MN��PQ�ֱ��ǡ�ABC�͡�AEF����λ�ߣ�
��MN=$\frac{1}{2}$AC��PQ=$\frac{1}{2}$AF��
��MN=PQ��
��2���⣺��BD=$\frac{1}{3}$BCʱ����M����N����P����QΧ�ɵ��ı����Ǿ��Σ�
����BE��MN��PQ����ͼ2��
�ߵ�M����Q��AB��AE���е㣮
��MQ��BE��MQ=$\frac{1}{2}$BE��
�ߵ�N��BC�е㣬
��BN=$\frac{1}{2}$BC��
�֡�BD=$\frac{1}{3}$BC��
��DN=BN-BD=$\frac{1}{2}$BC-$\frac{1}{3}$BC=$\frac{1}{6}$BC��
��$\frac{DN}{BD}$=$\frac{1}{2}$��
�ߵ�B���E����ֱ��AD�Գƣ�
��BE��AD��
ͬ��PN��AD��
��BE��PN��
���PDN�ס�EDB��
��$\frac{PN}{BE}$=$\frac{DN}{BD}$=$\frac{1}{2}$��
��MQ��PN��MQ=PN��
���ı���MQNP��ƽ���ı��Σ�
��MN=PQ��
���ı���MQNP�Ǿ��Σ�
��3����BD=0��3ʱ����M����N����P����QΧ�ɵ��������Σ�
��BD=2��6ʱ����M����N����P����QΧ�ɾ��Σ�
���� ���⿼�鼸�α任���⣬�ؼ��Ǹ���ȫ�������ε��ж������ʣ��Լ����������ε����ʽ��з�����ͬʱ���þ��ε��ж����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����AOB=45�㣬��0A�ϵ���O�ľ���ֱ�Ϊ1��3��5��7��9��11��L�ĵ���OA�Ĵ�����OB�ཻ���õ������һ���ɫ���Σ����ǵ�����ֱ�ΪS1��S2��S3��S4��L���۲�ͼ�еĹ��ɣ������11����ɫ���ε����S11=84��
��ͼ����AOB=45�㣬��0A�ϵ���O�ľ���ֱ�Ϊ1��3��5��7��9��11��L�ĵ���OA�Ĵ�����OB�ཻ���õ������һ���ɫ���Σ����ǵ�����ֱ�ΪS1��S2��S3��S4��L���۲�ͼ�еĹ��ɣ������11����ɫ���ε����S11=84���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ABCD�ı߳�Ϊ2����BAD=60�㣬�Խ���AC��BD�ཻ�ڵ�O������P���߶�AC�ϴӵ�A���C�˶�����P��PE��AD����AB�ڵ�E����P��PF��AB����AD�ڵ�F���ı���QHCK���ı���PEAF����ֱ��BD�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��AP=x��
����ABCD�ı߳�Ϊ2����BAD=60�㣬�Խ���AC��BD�ཻ�ڵ�O������P���߶�AC�ϴӵ�A���C�˶�����P��PE��AD����AB�ڵ�E����P��PF��AB����AD�ڵ�F���ı���QHCK���ı���PEAF����ֱ��BD�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��AP=x���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����O����B��C��Բ��O�ڵ���ֱ��������ABC���ڲ�����BAC=90�㣬OA=1��BC=6�����O�İ뾶Ϊ��������
��ͼ����O����B��C��Բ��O�ڵ���ֱ��������ABC���ڲ�����BAC=90�㣬OA=1��BC=6�����O�İ뾶Ϊ��������| A�� | 6 | B�� | 13 | C�� | $\sqrt{13}$ | D�� | 2$\sqrt{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����B��C��E��ͬһֱ���ϵ����㣬�ı���ABCD���ı���CEFG���������Σ�����BG��DE��
��ͼ����B��C��E��ͬһֱ���ϵ����㣬�ı���ABCD���ı���CEFG���������Σ�����BG��DE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com