
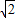 ,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.
,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.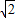 时,请求出直线PQ的解析式.
时,请求出直线PQ的解析式.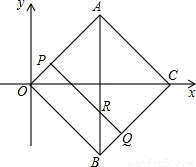
 OC,OD⊥CD,∠OAD=∠AOC=45°,AB=OC,∠OAC=90°,
OC,OD⊥CD,∠OAD=∠AOC=45°,AB=OC,∠OAC=90°,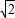 ,OA=AC=BC=OB=4,
,OA=AC=BC=OB=4,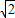 ,
,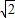 ,
, ,2
,2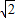 ),
),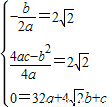 ,
, .
.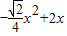 ;
;
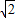
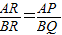

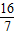
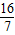 ,P(
,P(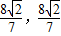 )
) ,Q(
,Q( )
)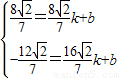
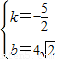
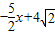 ;
;
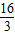
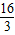 在整个运动过程中S与t的函数关系式有三种情况:
在整个运动过程中S与t的函数关系式有三种情况: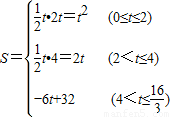


 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
| 2 |
| 2 |
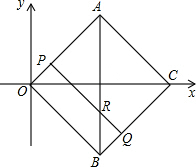 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
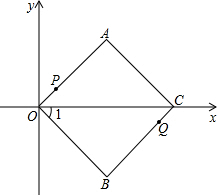 折线OACB方向匀速运动,另一动点Q从点C出发,沿折线CBOA方向匀速运动.
折线OACB方向匀速运动,另一动点Q从点C出发,沿折线CBOA方向匀速运动.查看答案和解析>>
科目:初中数学 来源: 题型:
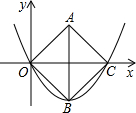 如图,已知抛物线y=(
如图,已知抛物线y=(| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t.
,0),动点P、Q同时从点O出发,点P沿着折线OACB的方向运动;点Q沿着折线OBCA的方向运动,设运动时间为t. 时,请求出直线PQ的解析式.
时,请求出直线PQ的解析式.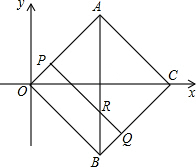 ,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.
,两点运动到相遇停止.设△OPQ的面积为S.请求出S关于t的函数关系式以及自变量t的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com