
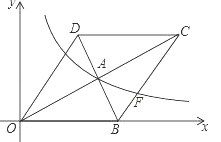
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
【答案】(12,![]() ).
).
【解析】
试题解析:过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,
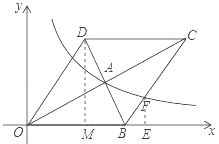
∵点D的坐标为(6,8),
∴OD=![]() =10,
=10,
∵四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为:(10,0),
∵AB=AD,即A是BD的中点,
∴点A的坐标为:(8,4),
∵点A在反比例函数y=![]() 上,
上,
∴k=xy=8×4=32,
∵OD∥BC,
∴∠DOM=∠FBE,
∴tan∠FBE=tan∠DOM=![]() ,
,
设EF=4a,BE=3a,
则点F的坐标为:(10+3a,4a),
∵点F在反比例函数y=![]() 上,
上,
∴4a(10+3a)=32,
即3a2+10a-8=0,
解得:a1=![]() ,a2=-4(舍去),
,a2=-4(舍去),
∴点F的坐标为:(12,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如果a+b<0,且ab>0,则下列结论成立的是:( )
A. a>0,b>0 B. a<0,b<0 C. a>0,b<0 D. a<0 ,b>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.
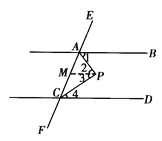
解:过P点作PM∥AB交AC于点M.
∵AB∥CD, ( )
∴∠BAC+∠ACD=180°. ( )
∵PM∥AB,
∴∠1=∠_______, ( )
且PM∥_______.(平行于同一直线的两直线也互相平行)
∴∠3=∠______. ( )
∵AP平分∠BAC,CP平分∠ACD, ( )
![]() BAC,
BAC, ![]() ACD.
ACD.
![]() .
.
∴∠APC=∠2+∠3=∠1+∠4=90°.
总结:两直线平行时,同旁内角的角平分线______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )
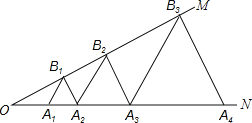
A.6 B.12 C.32 D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com