
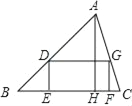
【题目】如图,△ABC是一块锐角三角形材料,高线AH长8cm,底边BC长10cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D、G分别在AB、AC上,AH交DG于M.
(1)求证:AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积能否等于25cm2?若能,求出宽DE的长度;否则,请说明理由.
【答案】(1)详见解析;(2)加工成的矩形零件DEFG的面积不能等于25cm2,理由详见解析.
【解析】试题分析:(1)根据矩形的对边平行得到DG∥EF,利用“平行于三角形的一边的直线截其他两边或其他两边的延长线,得到的三角形与原三角形相似”得到△ADG∽△ABC,再根据相似三角形对应高的比等于相似比得到![]() 然后利用比例的基本性质即可证明AMBC=AHDG;
然后利用比例的基本性质即可证明AMBC=AHDG;
(2)当加工成的矩形零件DEFG的面积等于![]() 时,设宽DE的长度为xcm,则AM=(8x)cm,
时,设宽DE的长度为xcm,则AM=(8x)cm, ![]() 根据(1)中结论AMBC=AHDG,列出方程
根据(1)中结论AMBC=AHDG,列出方程![]() 整理得
整理得![]() 进而求解即可.
进而求解即可.
试题解析:(1)证明:∵四边形DEFG为矩形,
∴DG∥EF,
∴△ADG∽△ABC,
∴![]()
∴AMBC=AHDG;
(2)加工成的矩形零件DEFG的面积不能等于![]() ,理由如下:
,理由如下:
当加工成的矩形零件DEFG的面积等于![]() 时,设宽DE的长度为xcm,则AM=(8x)cm,
时,设宽DE的长度为xcm,则AM=(8x)cm, ![]()
∵高线AH长8cm,底边BC长10cm,AMBC=AHDG,
∴![]()
整理得![]()
∵△=644×20=16<0,
∴x无实数根,
故加工成的矩形零件DEFG的面积不能等于![]() .
.



 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 ;
(2)补全频数分布直方图,求扇形图中“6吨﹣﹣9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算下列各题:
①2x2﹣4x+1+2x﹣5x2
②(8x﹣3x2)﹣5xy﹣2(3xy﹣2x2)
(2)先化简,再求值:(3x2y+5x)﹣[x2y﹣4(x﹣x2y)],其中(x+2)2+|y﹣3|=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解城市汽车交通拥堵,减少汽车尾气对大气的污染. 某区政府投放了大量公租自行车供市民使用. 到2016年底,全区已有公租自行车2 500辆,摆放点60个. 预计到2018年底,全区将有公租自行车5 000辆,并且平均每个摆放点的公租自行车数量是2016年底平均每个摆放点的公租自行车数量的1.2倍. 预计到2018年底,全区将有摆放点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD中,![]() ,
,![]() 绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线
绕点A顺时针旋转,它的两边长分别交CB、DC或它们的延长线![]() 于点MN,
于点MN,![]() 于点H.
于点H.
![]() 如图
如图![]() ,当
,当![]() 点A旋转到
点A旋转到![]() 时,请你直接写出AH与AB的数量关系;
时,请你直接写出AH与AB的数量关系;
![]() 如图
如图![]() ,当
,当![]() 绕点A旋转到
绕点A旋转到![]() 时,
时,![]() 中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.
中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形![]() 中,
中,![]() ,
,![]() 是对角线,点
是对角线,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上两个点,且满足
上两个点,且满足![]() ,连接
,连接![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2)如图2,作![]() 于
于![]() 点,求证:
点,求证:![]() ;
;
(3)在满足(2)的条件下,且点![]() 在菱形内部,若
在菱形内部,若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com