
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数;
(2)设∠BAD=θ,
①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.

【答案】(1)80°;(2)①10°,25°或40°;②5°或45°.
【解析】
试题分析:(1)由轴对称可以得出△ADB≌△ADF,就可以得出∠B=∠AFD,AB=AF,在证明△AGF≌△AGC就可以得出∠AFG=∠C,就可以求出∠DFG的值;
(2)①当GD=GF时,就可以得出∠GDF═80°,根据∠ADG=40+θ,就有40°+80°+40°+θ+θ=180°就可以求出结论;当DF=GF时,就可以得出∠GDF=50°,就有40°+50°+40°+2θ=180°,当DF=DG时,∠GDF=20°,就有40°+20°+40°+2θ=180°,从而求出结论;
②由已知条件可以得出∠DFG=80°,当∠GDF=90°时,就有40°+90°+40°+2θ=180°就可以求出结论,当∠DGF=90°时,就有∠GDF=10°,得出40°+10°+40°+2θ=180°求出结论.
试题解析:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠C=40°.
∵△ABD和△AFD关于直线AD对称,
∴△ADB≌△ADF,
∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,
∴AF=AC.
∵AG平分∠FAC,
∴∠FAG=∠CAG.
在△AGF和△AGC中,
AF=AC,∠FAG=∠CAG,AG=AG,
∴△AGF≌△AGC(SAS),
∴∠AFG=∠C.
∵∠DFG=∠AFD+∠AFG,
∴∠DFG=∠B+∠C=40°+40°=80°.
答:∠DFG的度数为80°;
(2)①当GD=GF时,
∴∠GDF=∠GFD=80°.
∵∠ADG=40°+θ,
∴40°+80°+40°+θ+θ=180°,
∴θ=10°.
当DF=GF时,
∴∠FDG=∠FGD.
∵∠DFG=80°,
∴∠FDG=∠FGD=50°.
∴40°+50°+40°+2θ=180°,
∴θ=25°.
当DF=DG时,
∴∠DFG=∠DGF=80°,
∴∠GDF=20°,
∴40°+20°+40°+2θ=180°,
∴θ=40°.
∴当θ=10°,25°或40°时,△DFG为等腰三角形;
②当∠GDF=90°时,
∵∠DFG=80°,
∴40°+90°+40°+2θ=180°,
∴θ=5°.
当∠DGF=90°时,
∵∠DFG=80°,
∴∠GDF=10°,
∴40°+10°+40°+2θ=180°,
∴θ=45°
∴当θ=5°或45°时,△DFG为直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( ).
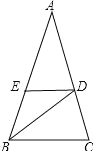
A.1个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四组条件中,能判定△ABC≌△DEF的是( )
A. AB=DE,BC= EF,∠A=∠D B. ∠A=∠D,∠C=∠F,AC= DE
C. ∠A=∠E,∠B=∠F,∠C=∠D D. AB=DE,BC= EF,△ABC的周长等于△DEF的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;④AD∥BE;且∠BAD=∠BCD.其中,能推出AB∥DC的条件为________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数y=
,反比例函数y=![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
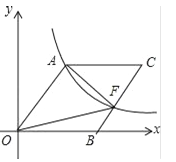
A. 60 B. 80 C. 30 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式的计算结果与x2m+2不相等的是( )
A. x2m·x2 B. xm-1·xm+3 C. x1-m·x3m+1 D. xm+2·x2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com