
分析 (1)先算二次根式,零指数幂,绝对值,乘方,负整数指数幂,再相加即可求解.
(2)①先确定分式方程的最简公分母为x(x+2),两边同乘最简公分母将分式方程转化为整式方程求解.
②先分别求出两个不等式的解,再求出公共解即可求解.
解答 解:(1)$\sqrt{4}$+(π-2)0-|-5|+(-1)2012+($\frac{1}{3}$)-2
=2+1-5+1+9
=8;
(2)①$\frac{5}{x+2}$=$\frac{3}{x}$,
5x=3(x+2),
5x=3x+6,
2x=6,
x=3;
②$\left\{\begin{array}{l}{4x+6>1-x①}\\{3(x-1)≤x+5②}\end{array}\right.$,
解不等式①得x>-1;
解不等式②得x≤4.
故不等式组的解集为-1<x≤4.
点评 考查了实数的运算,解分式方程和不等式组,解分式方程要注意:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:
如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.
如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
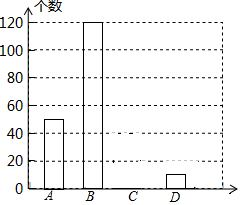 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:| 关注情况 | 频数 | 频率 |
| A.高度关注 | 50 | b |
| B.一般关注 | 120 | 0.6 |
| C.不关注 | a | 0.1 |
| D.不知道 | 10 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com