
 如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.分析 (1)由MN∥BC,易得∠CBN=∠MNB,由已知∠PNB=3∠CBN,根据角的和差不难得出结论;
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,由(1)知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可知∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
解答  解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN∥BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN;
(2)连接AN,
根据矩形的轴对称性,可知∠PAN=∠CBN,
∵MN∥AD,
∴∠PAN=∠ANM,
由(1)知∠PNM=2∠CBN,
∴∠PAN=∠PNA,
∴AP=PN,
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2,
设AP=x,则PD=6-x,
在Rt△PDN中
PD2+DN2=PN2,
∴(6-x)2+22=x2,
解得:x=$\frac{10}{3}$
所以AP=$\frac{10}{3}$.
点评 本题主要考查了矩形的性质、平行线的性质、等腰三角形的判定与性质、勾股定理的综合运用,难度不大,根据角的倍差关系得到∠PAN=∠PNA,发现AP=PN是解决问题的关键.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角相等,两条直线平行 | B. | 三条线段可以组成一个三角形 | ||
| C. | 平行于同一条直线的两条直线平行 | D. | 对顶角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
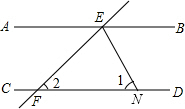 如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )
如图,直线AB∥CD,直线EF与AB,CD相交于点E,F,∠BEF的平分线与CD相交于点N.若∠1=63°,则∠2=( )| A. | 64° | B. | 63° | C. | 60° | D. | 54° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )
如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是($\frac{1}{2}$)2n+1ab.
如图,已知矩形ABCD的边长分别为a,b,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形I1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形I2;…如此操作下去,得到菱形In,则In的面积是($\frac{1}{2}$)2n+1ab.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
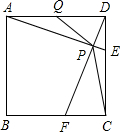 在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.
在边长为2cm的正方形ABCD中,动点E、F分别从D、C两点同时出发,都以1cm/s的速度在射线DC、CB上移动.连接AE和DF交于点P,点Q为AD的中点.若以A、P、Q为顶点的三角形与以P、D、C为顶点的三角形相似,则运动时间t为2或4秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com