
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到∠BOD=180°-54°=126°,然后由弧长的公式即可计算出结果.
试题解析:(1)连接OD,BD,
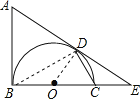
∵AB是⊙O的切线,∴AB⊥BC,即∠ABO=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°;
又∵OD是圆O的半径,∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠COD
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO=2∠CDE,
∴∠A=2∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°,
∵OB=2,∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 在﹣2.1和1.1之间的整数有3个B. 有最小的有理数
C. 3.6万精确到千位D. 数据258000用科学记数法可表示为258×103
查看答案和解析>>
科目:初中数学 来源: 题型:
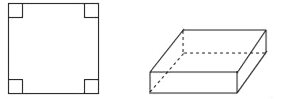
【题目】有一张边长为a厘米的大的正方形纸片,在它的四个角上各减去一个边长为x厘米的小正方形,折成一个无盖的长方体(如图).
(1)当a=9厘米时,请用含x的式子表示这个无盖长方体的体积.
(2)在(1)的条件下,当x=3厘米时求无盖长方体的体积;
(3)当a=12厘米时,要将这张正方形纸片折成一个无盖的正方体,求此时正方体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是马小哈同学做的一道题:
解方程:![]()
解:①去分母,得 4(2x﹣1)=1﹣3(x+2)
②去括号,得 8x﹣4=1﹣3x﹣6
③移项,得8x+3x=1﹣6+4
④合并同类项,得 11x=﹣1
⑤系数化为1,得![]()
(1)上面的解题过程中最早出现错误的步骤是(填代号) ;
(2)请在本题右边正确的解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,DE∥BC. 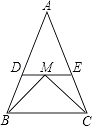
(1)试问△ADE是否是等腰三角形,说明理由;
(2)若M为DE上的点,且BM平分∠ABC,CM平分∠ACB,若△ADE的周长为20,BC=8.求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com