
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.

(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)x=3;(2)P点坐标为(3,![]() ).(3)N(
).(3)N(![]() ,﹣3)
,﹣3)
【解析】
试题分析:(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x﹣1)(x﹣5),代入A(0,4)即可求得函数的解析式,则可求得抛物线的对称轴;
(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,可求出直线BA′的解析式,即可得出点P的坐标.
(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
解:(1)根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上式得:a=![]() ,
,
∴y=![]() (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)=![]() x2﹣
x2﹣![]() x+4=
x+4=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ,
,
∴抛物线的对称轴是:x=3;
(2)P点坐标为(3,![]() ).
).
理由如下:
∵点A(0,4),抛物线的对称轴是x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4)
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.
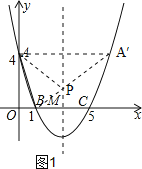
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得![]() ,
,
解得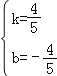 ,
,
∴y=![]() x﹣
x﹣![]() ,
,
∵点P的横坐标为3,
∴y=![]() ×3﹣
×3﹣![]() =
=![]() ,
,
∴P(3,![]() ).
).
(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
设N点的横坐标为t,此时点N(t,![]() t2﹣
t2﹣![]() t+4)(0<t<5),
t+4)(0<t<5),
如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,
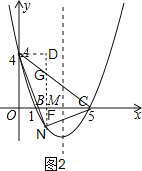
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣![]() x+4,
x+4,
把x=t代入得:y=﹣![]() t+4,则G(t,﹣
t+4,则G(t,﹣![]() t+4),
t+4),
此时:NG=﹣![]() t+4﹣(
t+4﹣(![]() t2﹣
t2﹣![]() t+4)=﹣
t+4)=﹣![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN=![]() AD×NG+
AD×NG+![]() NG×CF=
NG×CF=![]() NGOC=
NGOC=![]() ×(﹣
×(﹣![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为![]() ,
,
由t=![]() ,得:y=
,得:y=![]() t2﹣
t2﹣![]() t+4=﹣3,
t+4=﹣3,
∴N(![]() ,﹣3).
,﹣3).


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
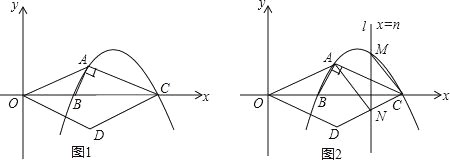
【题目】如图1,抛物线y=ax2-11ax+24a(a<0)与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.
(1)求线段OC的长和点B的坐标;
(2)连接OA,将△OAC沿x轴翻折后得△ODC,当四边形OACD是菱形时,求此时抛物线的解析式;
(3)如图2,折垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求这个最大值;
(4)在(3)的条件下,当取得最大值时,四边形ADNM是否为平行四边形?直接回答 (是或不是).如果不是,请直接写出此时的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由小亮家向东走20m,再向北走10m就到了小丽家,若再向北走30m就到了
小红家,再向东走40m,就到了小涛家.若用(0,0)表示小亮家的位置,用(2,1)表
示小丽家的位置.
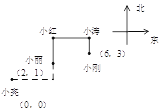
(1)小红、小涛家如何表示?
(2)小刚家的位置是(6,3),则小涛到小刚家怎么走?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于直线x=1对称的点是( )
A.点(0,-3)与点(-2,-3)
B.点(2,3)与点(0,3)
C.点(2,3)与点(-2,3)
D.点(2,3)与点(2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
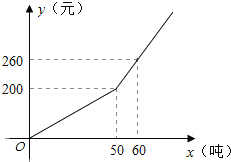
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收![]() 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
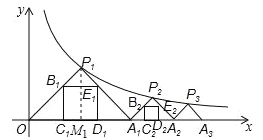
【题目】如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)在函数y=![]() (x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln= (用含n的式子表示).
(x>0)的图象上,△P1OA,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1,△P2A1A2的内接正方形的周长记为l2,…,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln,则l1+l2+l3+…+ln= (用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com