Question

已知直线y=2x+2与x轴交于点A，与y轴交于点M，点B与点A关于点M成中心对称，反比例函数的图象经过点B．
（1）求这个反比例函数的解析式；
（2）将这条直线平移，使它与反比例函数的图象交于点C，与y轴交于点D，如果BC∥AD，请求出平移的方向和距离；
（3）在第（2）小题的条件下，联结AC和BD，它们相交于点N，求△BCN的面积．

Answer 1

解：（1）把x=0代入y=2x+2得y=2；把y=0代入y=2x+2得2x+2=0，解得x=-1，则A点坐标为（-1，0）M点坐标为（0，2），
∵点B与点A关于点M成中心对称，
∴B点坐标为（1，4），
把B（1，4）代入得k=1×4=4，
∴反比例函数的解析式为y=；

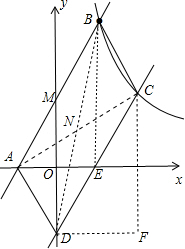
（2）如图，作BE⊥x轴于E，分别过C、D点作x轴、y轴的垂线，它们相交于F点，
∵AB∥DC，AD∥BC，
∴四边形ABCD为平行四边形，
∴AB=DC，
易证得Rt△ABE≌Rt△DCF，
∴DF=AE=2，CF=BE=4，
∴C点的横坐标为2，
把x=2代入y=得y=2，
∴OD=4-2=2，
∴D点坐标为（0，-2），
∴直线AB向下平移4个单位得到BC；

（3）∵四边形ABCD为平行四边形，
∴△BCN的面积=平行四边形ABCD的面积，
∵S_△ABD=S_△ADM+S_△BDM=×1×4+×1×4=4，
∴△BCN的面积=×2×4=2．
分析：（1）先确定A点坐标为（-1，0），M点坐标为（0，2），再根据中心对称的性质得到B点坐标为（1，4），然后运用待定系数法确定反比例函数的解析式；
（2）作BE⊥x轴于E，分别过C、D点作x轴、y轴的垂线，它们相交于F点，由于AB∥DC，AD∥BC，可判断四边形ABCD为平行四边形，则AB=DC，易证得Rt△ABE≌Rt△DCF，
得到DF=AE=2，CF=BE=4，即C点的横坐标为2，然后根据反比例函数解析式确定C点坐标，则OD=2，D点坐标为（0，-2），所以直线AB向下平移4个单位得到BC；
（3）根据平行四边形的性质得△BCN的面积=平行四边形ABCD的面积，然后计算S_△ABD=S_△ADM+S_△BDM=4，则△BCN的面积=×2×4=2．
点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、平行四边形的判定与性质．