

���� ��1��ֱ��д��DF=AF��
��2�����жϳ���ADC�ա�GDB���ó�BG=AC�����жϳ���AEF�ס�GBF�ó�����ʽ���ɵó����ۣ�
��3�������ڣ�2������������B��BG��AC���ó���ACD�ס�GBD���ɵó�BG=nAC��DG=nAD�������ó�FG=nAF+��n+1��DF�����á�BFG�ס�EFA���ó�����ʽ�����������ɵó����ۣ�
��� �⣺��1���ʴ�Ϊ��AF��
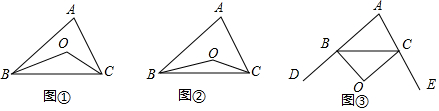
��2����ͼ1��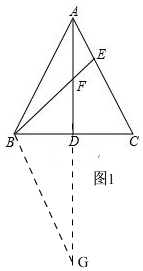 �ӳ�AD��G��ʹAD=DG������BG��
�ӳ�AD��G��ʹAD=DG������BG��
��AD�ǵȱ�������ABC�ı�BC�ϵĸߣ�
��BD=CD��
�ڡ�ADC�͡�GDB�У�$\left\{\begin{array}{l}{AD=DG}\\{��ADC=��GDB}\\{CD=BD}\end{array}\right.$��
���ADC�ա�GDB��
��BG=AC��
��CAD=��BGD��
��AC��BG��
���AEF�ס�GBF��
��$\frac{AE}{BG}=\frac{AF}{GF}$��
��AE=$\frac{1}{2}$EC��
��BG=AC=3AE��
��$\frac{AE}{3AE}=\frac{AF}{GF}$��
��FG=AG-AF=2AD-AF=2��AF+DF��-AF=AF+2DF��
��$\frac{AF}{AF+2DF}=\frac{1}{3}$��
��$\frac{AF}{2DF}=\frac{1}{2}$��
��DF=AF��
��3����ͼ��2����
����B��BG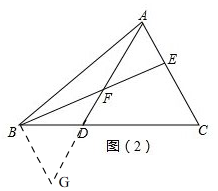 ��AC��AD���ӳ�����G��
��AC��AD���ӳ�����G��
���ACD�ס�GBD��
��$\frac{AC}{BG}=\frac{AD}{DG}=\frac{CD}{BD}$��
��BD=nDC��
��BG=nAC��DG=nAD=n��AF+DF����
��AE=mEC��
��AC=AE+EC=��m+1��EC��
��FG=DG+DF=n��AF+DF��+DF=nAF+��n+1��DF��
��BG��AC��
���BFG�ס�EFA��
��$\frac{FG}{AF}=\frac{BG}{AE}$=$\frac{nAC}{AE}$=$\frac{n��m+1��EC}{mEC}$=$\frac{n��m+1��}{m}$��
��$\frac{nAF+��n+1��DF}{AF}=\frac{n��m+1��}{m}$��
��n+$\frac{��n+1��DF}{AF}=\frac{n��m+1��}{m}$��
��$\frac{��n+1��DF}{AF}=\frac{n}{m}$��
��$\frac{DF}{AF}=\frac{n}{m��n+1��}$��
���� ���������������ε��ۺ��⣬��Ҫ������ȫ�������ε��ж������ʣ����������ε��ж������ʣ��Ȿ��Ĺؼ������������ߣ���������������Σ���һ���ܺõ��п������⣮


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
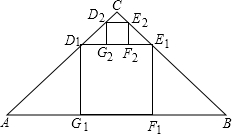 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=BC=2����Rt��ABC�ڲ���������D1E1F1G1�����е�D1��E1�ֱ���AC��BC���ϣ���F1G1��BC�ϣ������������S1����ͬ���ķ����ڡ�CD1E1�ڲ���������D2E2F2G2�������������S2��S2=$\frac{8}{{3}^{4}}$�������մ˹�������ȥ��������DnEnFnGn�����Sn=$\frac{8}{{3}^{2n}}$��
��ͼ����Rt��ABC�У���ACB=90�㣬AC=BC=2����Rt��ABC�ڲ���������D1E1F1G1�����е�D1��E1�ֱ���AC��BC���ϣ���F1G1��BC�ϣ������������S1����ͬ���ķ����ڡ�CD1E1�ڲ���������D2E2F2G2�������������S2��S2=$\frac{8}{{3}^{4}}$�������մ˹�������ȥ��������DnEnFnGn�����Sn=$\frac{8}{{3}^{2n}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Ϊ���� | B�� | ��Ϊ�෴�� | C�� | ��� | D�� | ��Ϊ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
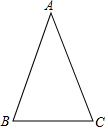 ��ͼ���ڡ�ABC�У�AB=AC��
��ͼ���ڡ�ABC�У�AB=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 70���20�� | B�� | 55���45�� | C�� | 55���35�� | D�� | 55���65�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com