
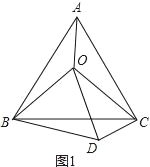
【题目】(1)如图1,O是等边△ABC内一点,连接OA、OB、OC,且OA=3,OB=4,OC=5,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.求:

①旋转角的度数;
②线段OD的长;
③∠BDC的度数.
(2)如图2所示,O是等腰直角△ABC(∠ABC=90°)内一点,连接OA、OB、OC,将△BAO绕点B顺时针旋转后得到△BCD,连接OD.当OA、OB、OC满足什么条件时,∠ODC=90°?请给出证明.
【答案】(1)①60°;②4;③150°;(2)OA2+2OB2=OC2时,∠ODC=90°,理由详见解析.
【解析】
(1)①△ABO旋转后AB与BC重合,根据旋转的性质可知∠ABC是旋转角,由△ABC是等边三角形即可知答案.②由旋转的性质可知OB=BD,根据旋转角是60°可知∠OBD=60°即可证明△BOD是等边三角形,进而求出OD的长.③根据OD=4,OC=5,CD=3可证明△OCD是直角三角形,根据△BOD是等边三角形即可求出∠BDC得度数.(2)根据旋转的性质可知旋转角为90°,可证明三角形BOD是等腰直角三角形,进而求出OD=![]() OB,根据△OCD是直角三角形即可知答案.
OB,根据△OCD是直角三角形即可知答案.
(1)①∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=60°,
∴旋转角的度数为60°;
②∵△BAO绕点B顺时针旋转后得到△BCD,
∴BO=BD,
而∠OBD=60°,
∴△OBD为等边三角形;
∴OD=OB=4;
③∵△BOD为等边三角形,
∴∠BDO=60°,
∵△BAO绕点B顺时针旋转后得到△BCD,
∴CD=AO=3,
在△OCD中,CD=3,OD=4,OC=5,
∵32+42=52,
∴CD2+OD2=OC2,
∴△OCD为直角三角形,∠ODC=90°,
∴∠BDC=∠BDO+∠ODC=60°+90°=150°;
(2)OA2+2OB2=OC2时,∠ODC=90°.理由如下:
∵△BAO绕点B顺时针旋转后得到△BCD,
∴∠OBD=∠ABC=90°,BO=BD,CD=AO,
∴△OBD为等腰直角三角形,
∴OD=![]() OB,
OB,
∵当CD2+OD2=OC2时,△OCD为直角三角形,∠ODC=90°,
∴OA2+2OB2=OC2,
∴当OA、OB、OC满足OA2+2OB2=OC2时,∠ODC=90°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:
(1)货车在乙地卸货停留了多长时间?
(2)货车往返速度,哪个快?返回速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为12cm2,则S△DGF的值为( )

A.4cm2 B.6cm2 C.8cm2 D.9cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
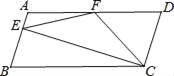
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF、EC,且CF=EF,下列结论正确的个数是( )
①CF平分∠BCD;②∠EFC=2∠CFD;③∠ECD=90°;④CE⊥AB.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 . 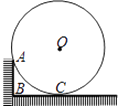
查看答案和解析>>
科目:初中数学 来源: 题型:
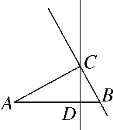
【题目】如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发在直线BC上以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.当点E运动________s时,CF=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=26°,∠C=70°,AD平分∠BAC,
AE⊥BC于点E,EF⊥AD于点F.
(1)求∠DAC的度数;
(2)求∠DEF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com