
【题目】阅读小强同学数学作业本上的截图内容并完成任务:
解方程组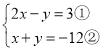
解:由①,得![]() ,③ 第一步
,③ 第一步
把③代入①,得![]() .第二步
.第二步
整理得,![]() .第三步
.第三步
因为![]() 可以取任意实数,所以原方程组有无数个解 第四步
可以取任意实数,所以原方程组有无数个解 第四步
任务:(1)这种解方程组的方法称为 ;
(2)利用此方法解方程组的过程中所体现的数学思想是 ;(请你填写正确选项)
A.转化思想 B.函数思想 C.数形结合思想 D.公理化思想
(3)小强的解法正确吗? (填正确或不正确),如果不正确,请指出错在第 步,请选择恰当的解方程组的方法解该方程组.
【答案】(1)代入法;(2)A;(3)不正确,第二步,见解析.
【解析】
(1)根据“把③代入①”可以判定出解方程组的方法;
(2)利用解方程组的方法代入消元法可以判断出所体现的数学思想;
(3)用代入消元法解方程组时,不能将转化所得的第三个方程带回转化前的原方程中,故可以判断出解法不正确,进而判断出哪一步错误;利用加减消元法解出方程组即可.
解:(1)代入法(或“代入消元法”)
由第一步、第二步的解题过程可以看出是代入消元法的方法;
(2)A
∵利用了代入消元法解方程组,∴体现的数学思想是转化思想;
(3)不正确;第二步
∵在用代入消元法解方程组的时候,我们不能将所得到的第三个方程带回到转化前的原方程中,
∴这种方法是不正确的;
∵第一步是由①得![]() ③,第二步是把③代入①,
③,第二步是把③代入①,
∴第二步是错误的;
正确解法:
①+②,得![]() ,解得,
,解得,![]() ,
,
把![]() 代入①,得
代入①,得![]() ,
,
则方程组的解为:![]() .
.


 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.请完成说明过程.
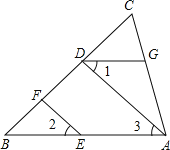
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代换)
∴AB∥ ,( )
∴∠DGA+∠BAC=180°.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
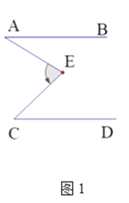
【题目】如图,AB∥CD.
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,![]()
![]() ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
(1)如图1,求证:A、G、E、F四点围成的四边形是菱形;
(2)如图2,点N是线段BC的中点,且ON=OD,求折痕FG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com