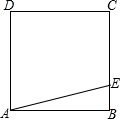
有一块边长为40米的正方形绿地ABCD.如图所示.在绿地旁边E处有健身器材.BE=9米．由于居住在A处的居民去健身践踏了绿地.小明想在A处树立一个标牌“少走■米.踏之何忍．请你计算后帮小明在标牌的■处填上适当的数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

8．

有一块边长为40米的正方形绿地ABCD，如图所示，在绿地旁边E处有健身器材，BE=9米．由于居住在A处的居民去健身践踏了绿地，小明想在A处树立一个标牌“少走■米，踏之何忍”．请你计算后帮小明在标牌的■处填上适当的数．

分析直接利用勾股定理得出AE的长，再求出AB+BE，即可得出答案．

解答解：在 Rt△ABE中，由勾股定理得：AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{4{0}^{2}+{9}^{2}}$=41，
而AB+BE=40+9=49，
因为49-41=8，所以标牌上填的数是8．

点评此题主要考查了勾股定理的应用，正确得出AE的长是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

18．计算：${|{-\frac{3}{4}}|^2}÷{（-1\frac{1}{2}）^3}+{（-1）^{2004}}×|{\frac{1}{2}-\frac{1}{3}}|$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

19．

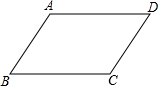对四边形ABCD加条件，使之成为平行四边形，下面的添加不正确的是（　　）

A．

AB=CD，AB∥CD

B．

AB∥CD，AD=BC

C．

AB=CD，AD=BC

D．

AC与BD相互平分

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．解方程：$\frac{x+1}{x-1}$=$\frac{x}{x+1}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

在平面直角坐标系中，△ABO的三个顶点坐标分别为：A（2，3）、B（3，1）、O（0，0）．
（1）将△ABO向左平移4个单位，画出平移后的△A₁B₁O₁．
（2）将点O为对称中心，画出与△ABO成中心对称的△A₂B₂O．此时四边形ABA₂B₂的形状是平行四边形．
（3）在平面上是否存在点D，使得以A、B、O、D为顶点的四边形是平行四边形，若存在请直接写出符合条件的所有点的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动．对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计表和统计图（图中信息不完整）．已知A、B两组捐款户数的比为1：5．

捐款户数分组统计表

组别	捐款额（x）元	户数
A	1≤x＜50	a
B	50≤x＜100	10
C	100≤x＜150	20
D	150≤x＜200	14
E	x≥200	4

请结合以上信息解答下列问题．
（1）a=2，本次调查样本的容量是50；
（2）补全“捐款户数分组统计表和捐款户数分组统计图1”；
（3）若该社区有1500户住户，请根据以上信息，估计全社区捐款不少于150元的户数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．解方程（不等式）组
（1）解方程组$\left\{\begin{array}{l}3（{x-1}）=y+5\\ 5（{y-1}）=3（{x+5}）\end{array}\right.$
（2）解不等式组$\left\{\begin{array}{l}1-2（{x-1}）＞x\\ \frac{x-1}{3}≥\frac{x+1}{4}-1\end{array}\right.$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．先化简，再求值：
（1）6a²-（2a-1）（3a+2）+（a+2）（a-2），其中a=-$\sqrt{2}$
（2）$\frac{x-3}{2x-4}$÷（$\frac{5}{x-2}$-x-2），其中x=$\sqrt{3}$-3．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．为了传承中华优秀传统文化，某校组织了一次七年级的“汉字听写”大赛，七年级1班学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，同学们把成绩进行整理，得到下列表格：

成绩（分）	50	60	70	80	90	100
人数	2	6	9	18	13	2

（1）七年级1班有50名学生；
（2）请选择一种统计图将整理的结果表示出来；
（3）七年级2班的成绩整理如下表：

成绩（分）	50	60	70	80	90	100
人数	6	9	7	9	15	4

请你谈谈哪个班的比赛成绩好些，并说明理由．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学