分析:本题应先根据题意把解不等式转化为求函数取值范围的问题,令y1=4x+3,y2=x+9,根据题意画出图象便可直接解答.
解答: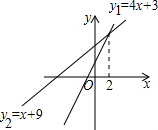
解:令y
1=4x+3,y
2=x+9,
对于y
1=4x+3,当x=0时,y=3;当y=0时,x=-
,
即y
1=4x+3过点(0,3)和点(-
,0),过这两点作直线即为y
1=4x+3的图象;
对于y
2=x+9,当x=0时,y=9;当y=0时,x=-9,
即y
2=x+9过点(0,9)和点(-9,0),过这两点作直线即为y
2=x+9的图象.
图象如上图:
由图可知当x<2时,不等式4x+3<x+9成立.
点评:本题考查的是函数与不等式解的关系,把求不等式解的问题转化成一次函数的问题,由其图象解答.

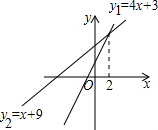 解:令y1=4x+3,y2=x+9,
解:令y1=4x+3,y2=x+9,
