
【题目】四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.

(1)利用图1,求证:四边形ABCD是菱形.
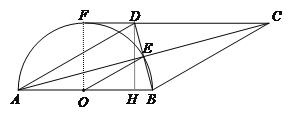
(2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
①连结OE,求△OBE的面积.
②求弧AE的长.
【答案】(1)证明见解析;(2)①4,②p.
【解析】试题分析: (1)利用对角线互相平分可先判断四边形ABCD为平行四边形,再利用直径对的圆周角是90°可得到AC⊥BD,就可判断是菱形.(2)①连接OF,可得OF为△ABD边AB上的高,可求得△ABD的面积为16,△AEB面积为△ABD的面积的一半,即等于8,△OEB的面积为△AEB面积的一半,即等于4;④过点D作DH⊥AB于点H.可得四边形OFDH为矩形,在Rt△ADH中利用三角函数可求得∠DAH=30°,进而可求得∠AOE的度数,弧AE的长度可求.
试题解析:(1)∵AE="EC,BE=ED," ∴四边形ABCD是平行四边形.∵AB为直径,且过点E,∴∠AEB=90°,即AC⊥BD.而四边形ABCD是平行四边形,∴四边形ABCD是菱形.(2)①连结OF.∵CD的延长线与半圆相切于点F,∴OF⊥CF.∵FC∥AB,∴OF即为△ABD的AB边上的高.S△ABD=AB×OF=×8×4=16.∵点O,E分别是AB,BD的中点,∴S△ABE=S△ABD=8,所以,S△OBE=S△ABE=4.②过点D作DH⊥AB于点H.∵AB∥CD,OF⊥CF,
∴FO⊥AB,∴∠F=∠FOB=∠DHO=90°.∴四边形OHDF为矩形,即DH=OF=4.在Rt△DAH中,sin∠DAB=![]() =,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=
=,∴∠DAH=30°.∵点O,E分别为AB,BD中点,∴OE∥AD,∴∠EOB=∠DAH=30°.∴∠AOE=180°-∠EOB=150°.∴弧AE的长=![]() .
.


科目:初中数学 来源: 题型:
【题目】据《天津日报》报道,天津市社会保障制度更加成熟完善,截止2017年4月末,累计发放社会保障卡12630000张.将12630000用科学记数法表示为( )
A.0.1263×108
B.1.263×107
C.12.63×106
D.126.3×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工.如图的线段和折线是两队前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象
根据图象解答下列问题:
(1)直接写出y甲、y乙(米)与x(天)之间的函数关系式.
①当0<x≤6时,y甲=;
②当0<x≤2时,y乙=;当2<x≤6时,y乙=;
(2)求图中点M的坐标,并说明M的横、纵坐标表示的实际意义;
(3)施工过程中,甲队的施工速度始终不变,而乙队在施工6天后,每天的施工速度提高到120米/天,预计两队将同时完成任务.两队还需要多少天完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com