
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
【答案】(1)需要12天完工;(2)由乙队单独施工花钱少,理由见解析.
【解析】试题分析:(1)设需要x天完工,根据等量关系:施工效率×时间=工作总量,列方程进行求解即可;
(2)分三种情况:甲单独、乙单独、甲乙合作,分别求出每种情况的费用,进行比较即可得出施工费用最少的那个方案.
试题解析:(1)设需要x天完工,由题意得![]() x+
x+![]() x=1 ,
x=1 ,
解得:x=12 ,
答:需要12天完工;
(2)由乙队单独施工花钱少,
理由:甲单独施工需付费:200×30=6000(元),
乙单独施工需付费:280×20=5600(元),
两队同时施工需付费:(200+280)×12=5760(元),
因为5600<5760<6000, 所以由乙队单独施工花钱少.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.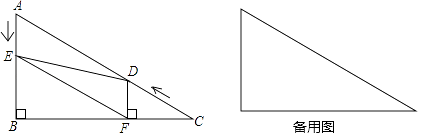
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
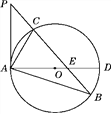
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG·AB=12,求AC的长;(3)在满足(2)的条件下,若AF∶FD=1∶2,GF=1,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘2018年初房价为每平方米20000元,经过两年连续降价后,2020 年初房价为16200元。设该楼盘这两年房价年平均降低的百分率为x,根据题意可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com