
����ʦҪ��ѧ�����б��⣬���н���ѵ��������С��ͬѧ�����ϰ���ǣ�
��![]() ��3������
��3������![]() ������ʵ������
������ʵ������![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
С��ͬѧ�������Ľ������ǣ�
�⣺��![]() ��3
��3
�� ��֪������![]()
�֡�
�� ![]() ��
��![]()
�� ![]() ��1��
��1��
(1
������������ϵ���ϰ��ͽ������������жϣ��ټ������ɣ�(2
������ֻ��С��ͬѧ�������ϰ���е� ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x2 |
| x1 |
| x1 |
| x2 |
| x2 |
| x1 |
| x1 |
| x2 |
| ||||
| x1•x2 |
| (x1+x2)2-2x1x2 |
| x1•x2 |
| 32-2��3 |
| 3 |
| 9-6 |
| 3 |
| x2 |
| x1 |
| x1 |
| x2 |
| x1+x2 |
| x1•x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֵ��
��ֵ�� =
=
 =1��
=1��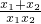 ��ֵ��
��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012��ɽ��ʡΫ���������������п���ѧģ���Ծ��������棩 ���ͣ������
 ��ֵ��
��ֵ�� =
=
 =1��
=1�� ��ֵ��
��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2003��ȫ���п���ѧ�����ࡶһԪ���η��̡���04���������棩 ���ͣ������
 ��ֵ��
��ֵ�� =
=
 =1��
=1�� ��ֵ��
��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2003��㶫ʡï�����п���ѧ�Ծ��������棩 ���ͣ������
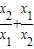 ��ֵ��
��ֵ��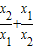 =
=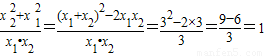
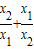 =1��
=1��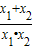 ��ֵ��
��ֵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com