
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,以点
,以点![]() 为顶点作
为顶点作![]() ,使得
,使得![]() ,交
,交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.

(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,且
,且![]() ,求
,求![]() 的半径.
的半径.
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
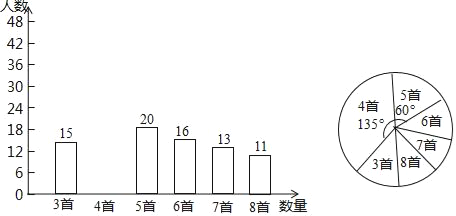
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
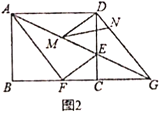
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求![]() 的值;
的值;
(2)求证:四边形![]() 是菱形;
是菱形;
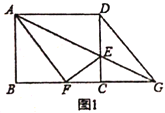
(3)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() ,设
,设![]() ,
,![]() ,请解决以下相关问题:
,请解决以下相关问题:
①写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形![]() 的对角线交于点
的对角线交于点![]() 是直线
是直线![]() 上任意一点(异于点
上任意一点(异于点![]() ),过点
),过点![]() 作平行于
作平行于![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,如图 ①,易证:
上时,如图 ①,易证:![]() (不用证明);
(不用证明);
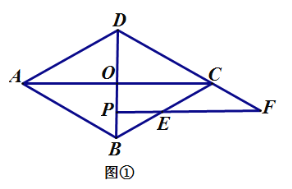
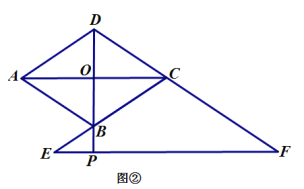
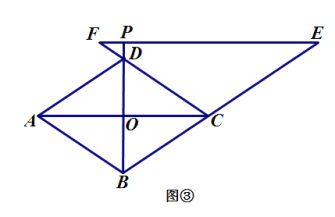
(2)当点![]() 在线段
在线段![]() 的延长线上时,如图 ②;当点
的延长线上时,如图 ②;当点![]() 在线段
在线段![]() 的延长线上时,如图 ③,线段
的延长线上时,如图 ③,线段![]() 之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
之间又有怎样的数量关系? 请写出你的猜想,并选择其中一种情况加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划新购进![]() 、
、![]() 两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中
两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中![]() 种苗的单价为
种苗的单价为![]() 元/棵,购买
元/棵,购买![]() 种苗所需费用
种苗所需费用![]() (元)与购买数量
(元)与购买数量![]() (棵)之间存在如图所示的函数关系.
(棵)之间存在如图所示的函数关系.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若在购买计划中,![]() 种苗的数量不超过35棵,但不少于
种苗的数量不超过35棵,但不少于![]() 种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
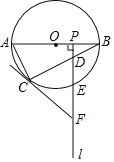
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)当点![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
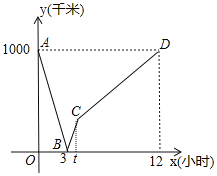
【题目】一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为![]() (小时),两车之间的距离为
(小时),两车之间的距离为![]() (千米),如图中的折线表示
(千米),如图中的折线表示![]() 与
与![]() 之间的函数关系,下列说法:①动车的速度是
之间的函数关系,下列说法:①动车的速度是![]() 千米/小时;②点B的实际意义是两车出发后
千米/小时;②点B的实际意义是两车出发后![]() 小时相遇;③甲、乙两地相距
小时相遇;③甲、乙两地相距![]() 千米;④普通列车从乙地到达甲地时间是
千米;④普通列车从乙地到达甲地时间是![]() 小时,其中不正确的有( )
小时,其中不正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
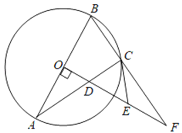
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
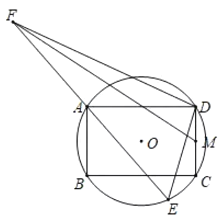
【题目】如图,⊙O的半径为![]() ,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
,四边形ABCD为⊙O的内接矩形,AD=6,M为DC中点,E为⊙O上的一个动点,连结DE,作DF⊥DE交射线EA于F,连结MF,则MF的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com