Question

【题目】Rt△ABC中，AB＝AC，D点为Rt△ABC外一点，且BD⊥CD，DF为∠BDA的平分线，当∠ACD＝15°，下列结论：①∠ADC＝45°；②AD＝AF；③AD+AF＝BD；④BC﹣CE＝2D,其中正确的是( )

A.①③B.①②④C.①③④D.①②③④

Answer 1

【答案】C

【解析】

由题意可证点A，点C，点B，点D四点共圆，可得∠ADC＝∠ABC＝45°；由角平分线的性质和外角性质可得∠AFD＝∠BDF+∠DBF＞∠ADF，可得AD≠AF；如图，延长CD至G，使DE＝DG，在BD上截取DH＝AD，连接HF，由“SAS”可证△ADF≌△HDF，可得∠DHF＝∠DAF＝30°，AF＝HF，由等腰三角形的性质可得BH＝AF，可证BD＝BH+DH＝AF+AD；由“SAS”可证△BDG≌△BDE，可得∠BGD＝∠BED＝75°，由三角形内角和定理和等腰三角形的性质可得BC＝BG＝2DE+EC.

∵AB＝AC，∠BAC＝90°，

∴∠ABC＝∠ACB＝45°，且∠ACD＝15°，

∵∠BCD＝30°，

∵∠BAC＝∠BDC＝90°，

∴点A，点C，点B，点D四点共圆，

∴∠ADC＝∠ABC＝45°，故①符合题意，

∠ACD＝∠ABD＝15°，∠DAB＝∠DCB＝30°，

∵DF为∠BDA的平分线，

∴∠ADF＝∠BDF，

∵∠AFD＝∠BDF+∠DBF＞∠ADF，

∴AD≠AF，故②不合题意，

如图，延长CD至G，使DE＝DG，在BD上截取DH＝AD，连接HF，

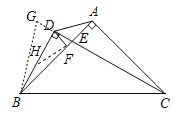
∵DH＝AD，∠HDF＝∠ADF，DF＝DF，

∴△ADF≌△HDF(SAS)

∴∠DHF＝∠DAF＝30°，AF＝HF，

∵∠DHF＝∠HBF+∠HFB＝30°，

∴∠HBF＝∠BFH＝15°，

∴BH＝HF，

∴BH＝AF，

∴BD＝BH+DH＝AF+AD，故③符合题意，

∵∠ADC＝45°，∠DAB＝30°＝∠BCD，

∴∠BED＝∠ADC+∠DAB＝75°，

∵GD＝DE，∠BDG＝∠BDE＝90°，BD＝BD，

∴△BDG≌△BDE(SAS)

∴∠BGD＝∠BED＝75°，

∴∠GBC＝180°﹣∠BCD﹣∠BGD＝75°，

∴∠GBC＝∠BGC＝75°，

∴BC＝BG，

∴BC＝BG＝2DE+EC，

∴BC﹣EC＝2DE，故④符合题意，

故选：C.