
 如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,现准备把坡角降为∠CAD=15°.
如图,有一段斜坡BC长为30米,坡角∠CBD=30°,为方便车辆通行,现准备把坡角降为∠CAD=15°.分析 (1)根据题意和直角三角形中30°角所对的直角边等于斜边的一半,可以求得CD的长;
(2)根据题意可以求得∠ACD=75°,也可以求得AD和CD的长,从而可以解答本题.
解答 解:(1)∵∠CDB=90°,∠CBD=30°,BC=30米,
∴CD=15米,
即坡高CD为15米;
(2))∵∠CDB=90°,∠CBD=30°,∠CAD=15°,
∴∠BCD=60°,∠BCA=15°,
∴∠ACD=75°,AB=BC,
∵BC=30米,
∴AB=30米,BD=BC•sin60°=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$米,CD=15米,
∴tan∠ACD=$\frac{AD}{CD}=\frac{30+15\sqrt{3}}{15}=2+\sqrt{3}$,
即tan75°=2+$\sqrt{3}$.
点评 本题考查解直角三角形的应用-坡度坡角问题,解题的关键是明确题意,找出所求问题需要的条件,利用锐角三角函数进行解答.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号).
如图,一艘轮船在A处测得北偏东45°方向有一灯塔B,船向正东方向航行到达C处时,又观测到灯塔B在北偏东30°方向上,此时轮船与灯塔相距60海里,求轮船从A处到C处航行了多少海里(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2002 年国际数学家大会在中国北京举行,这是21 世纪全世界数学家的第一次大聚会.这次大会的会徽就是如图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?
2002 年国际数学家大会在中国北京举行,这是21 世纪全世界数学家的第一次大聚会.这次大会的会徽就是如图,选定的是我国古代数学家赵爽用来证明勾股定理的弦图,可以说是充分肯定了我国数学的成就,也弘扬了我国古代的数学文化.弦图是由四个全等的直角三角形和中间的 小正方形拼成的一个大正方形.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么你能求出(a+b)2 的值吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
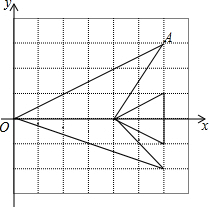 如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的$\frac{1}{2}$,那么点A对应的点A′的坐标是(3,3).
如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标变为原来的$\frac{1}{2}$,那么点A对应的点A′的坐标是(3,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com