
分析 (1)设水果店第一次购进这种橙子每干克的价格是x元,则第二次购进这种橙子每千克的价格是1.25x元,根据数量=总价÷单价结合第二次购进的数量比第一次少50千克,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)根据数量=总价÷单价求出11月份购买的橙子数量,再根据单价×数量=总价结合12月进货总价比11月进货总价多550元,即可得出关于a的一元二次方程,解之即可得出结论.
解答 解:(1)设水果店第一次购进这种橙子每干克的价格是x元,则第二次购进这种橙子每千克的价格是1.25x元,
根据题意得:$\frac{800}{x}$-$\frac{750}{1.25x}$=50,
解得:x=4,
经检验,x=4是原方程的解,且符合题意.
答:水果店第一次购进这种橙子每干克的价格是4元.
(2)11月份购进橙子800÷4×2-50=350(千克).
根据题意得:350(1+4a%)×4(1+5a%)=800+750+550,
整理得:40(a%)2+18a%-1=0,
解得:a%=$\frac{1}{20}$或a%=-$\frac{1}{2}$(舍去),
∴a=5.
答:a的值为5.
点评 本题考查了分式方程的应用以及一元二次方程的应用,解题的关键是:(1)根据数量=总价÷单价结合第二次购进的数量比第一次少50千克,列出关于x的分式方程;(2)根据单价×数量=总价结合12月进货总价比11月进货总价多550元,列出关于a的一元二次方程.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | x>-1 | B. | x≥-1 | C. | x≥-1且x≠2 | D. | x>-1且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 质量(g) | 73 | 74 | 75 | 76 | 77 | 78 |
| 甲的数量 | 2 | 4 | 4 | 3 | 1 | 1 |
| 乙的数量 | 2 | 3 | 6 | 2 | 1 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
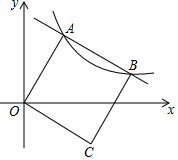 如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com