
分析 (1)由2$\sqrt{x}$×$\sqrt{x}$=2x,即可找出2$\sqrt{x}$的有理化因式;
(2)①分式中分子、分母同时×($\sqrt{7}$-$\sqrt{6}$),即可得出结论;②分式中分子、分母同时×(3$\sqrt{2}$-$\sqrt{17}$),即可得出结论;
(3)利用分母有理化将原式变形为$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+$\sqrt{n+1}$-$\sqrt{n}$,合并同类项即可得出结论.
解答 解:(1)∵2$\sqrt{x}$×$\sqrt{x}$=2x,
∴2$\sqrt{x}$的有理化因式是$\sqrt{x}$.
故答案为:$\sqrt{x}$.
(2)①$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{\sqrt{7}-\sqrt{6}}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$;
②$\frac{1}{3\sqrt{2}+\sqrt{17}}$=$\frac{3\sqrt{2}-\sqrt{17}}{(3\sqrt{2}+\sqrt{17})(3\sqrt{2}-\sqrt{17})}$=3$\sqrt{2}$-$\sqrt{17}$.
故答案为:①$\sqrt{7}$-$\sqrt{6}$;3$\sqrt{2}$-$\sqrt{17}$.
(3)原式=$\frac{\sqrt{2}-1}{(1+\sqrt{2})(\sqrt{2}-1)}$+$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$+…+$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$,
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+$\sqrt{n+1}$-$\sqrt{n}$,
=$\sqrt{n+1}$-1.
点评 本题考查了分母有理化,解题的关键是:(1)由2$\sqrt{x}$×$\sqrt{x}$=2x,找出2$\sqrt{x}$的有理化因式;(2)根据平方差公式,将各式分母有理化;(3)利用分母有理化将原式变形为$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+2-$\sqrt{3}$+…+$\sqrt{n+1}$-$\sqrt{n}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
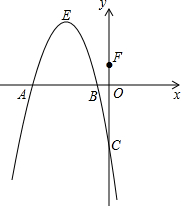 如图,抛物线y=-x2+bx+c交x轴于A,B两点,交y轴于点C,对称轴是直线x=-3,B(-1,0),F(0,1),请解答下列问题:
如图,抛物线y=-x2+bx+c交x轴于A,B两点,交y轴于点C,对称轴是直线x=-3,B(-1,0),F(0,1),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
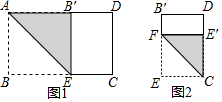 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):查看答案和解析>>
科目:初中数学 来源: 题型:填空题
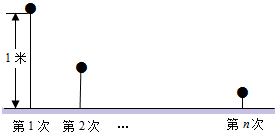 一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.
一小球从距地面1m高处自由落下,每次着地后又跳回到原高度的一半再落下.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
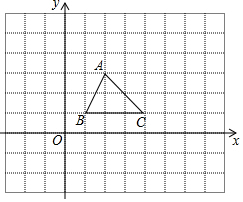 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:
如图,在正方形ABCD外取一点E,连接AE,DE,BE,过点A作AE的垂线交ED于点P,连接BP,AE=AP=1,PB=$\sqrt{5}$,有下列结论:| A. | ①③④ | B. | ①②⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com