
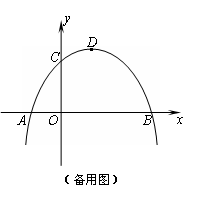
��ͼ�������� �Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��
�Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��
��1����a��b��ֵ��
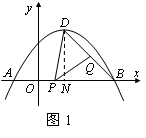
��2����45��ǵĶ���P���߶�OB�ϻ���(�����B�غ�)���ýǵ�һ�߹���D����һ����BD���ڵ�Q����P��x��0����y2= DQ�������y2����x�ĺ�����ϵʽ��
DQ�������y2����x�ĺ�����ϵʽ��
��3����ͬһƽ��ֱ������ϵ�У�����ֱ��x = m��x = m+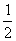 �ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ
�ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ �����ܣ����m��ֵ�������ܣ���˵�����ɣ�
�����ܣ����m��ֵ�������ܣ���˵�����ɣ�
 |  | ||
�⣺��1����拋����y1=ax2-2ax+b����B(3��0)��C(0��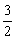 )���㣬
)���㣬
��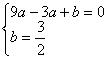 ����
����
��拋���ߵĽ���ʽΪy1= -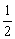 x2+x+
x2+x+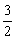 �� ---------4��
�� ---------4��
��2����DN^AB������ΪN��������ͼ1��
��y1= -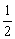 x2+x+
x2+x+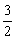 ��D(1��2)
��D(1��2)
N(1��0)��A(-1��0)��B(3��0)����AB=4��DN=BN=2��DB=2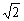 ��
��
ÐDBN=45�㣮���ݹ��ɶ�����BD 2-BN 2=PD 2-PN 2��
��(2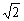 )2-22=PD2-(1-x)2-----j
)2-22=PD2-(1-x)2-----j
��ÐMPQ=45��=ÐMBP��
���MPQ �� ��MBP����PD2=DQ´DB=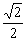 y2´2
y2´2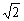 ------k��
------k��
��j��k��y2=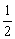 x2-x+
x2-x+ ����0��x��3��
����0��x��3��
��y2��x�ĺ�����ϵʽΪy2=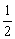 x2-x+
x2-x+ =
=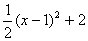
 (0��x��3)��--------4��
(0��x��3)��--------4��
���Ա���ȡֵ��Χûд�����۷֣�
 | |||
 | |||
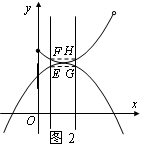
��3������E��F��H��GΧ���ı��ε������Ϊ ����ͼ2��
����ͼ2��
�ߵ�E��G��������y1= -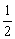 x2+x+
x2+x+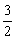 =
=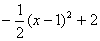 �ֱ���ֱ��x=m��x= m+
�ֱ���ֱ��x=m��x= m+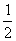 �Ľ���
�Ľ���
���E��G����Ϊ E(m��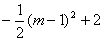 )��G(m+
)��G(m+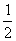 ��
��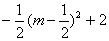 )��
)��
ͬ������F��H���� ΪF(m��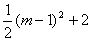 )��H(m+
)��H(m+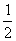 ��
��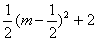 )��
)��
��EF=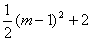 -��
-��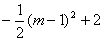 ��=
��=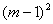
GH=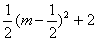 )-��
)-��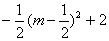 ��=
��= ��
��
���ı���EFHG��ƽ���ı��λ����Σ�
��S=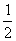 ��
��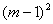 +
+ �ݡ�
�ݡ�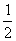 =
=
�����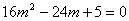
���m=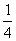 ��
�� ������0��x��3�ڣ�
������0��x��3�ڣ�
���ԣ���m=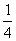 ��
�� ʱ��E��F��H��GΧ���ı��ε����Ϊ
ʱ��E��F��H��GΧ���ı��ε����Ϊ .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�߹���ͼ��������ͼ�ۼ�����д������
��ͼ����֪�߶� a, h ��������aΪ�ס�hΪ�ߵĵ���������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���㵺���丽���������ҹ��Ĺ���������̨�屣����ʿ
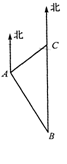
����ǰ�����㵺����ʾ��Ȩ��������������������B��ʱ����ͼ����
��õ��㵺λ����������20�����C����Ϊ�˷�ֹ�ձ���Ѳ�����ţ�
��������A���ĺ��ബǰ��C����������֪C��λ��A���ı�ƫ��45��
�ķ����ϣ� Aλ��B�ı�ƫ��30��ķ����ϣ�
��A��C֮��ľ���? �������ȷ��0.1����ο����ݣ�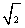 ��1.41��
��1.41��
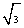 ��1.73����
��1.73����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��������y=��x��1��2+3����ƽ��1����λ���õ�����������y��Ľ��������ǣ�������
| �� | A�� | ��0��2�� | B�� | ��0��3�� | C�� | ��0��4�� | D�� | ��0��7�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij����Ʒÿ���ı��Ϊ240Ԫ������۵İ�������ʱ��ÿ�����ܻ���20%����������Ʒÿ���Ľ���Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com