
【题目】如图,已知:AD平分∠CAE,AD∥BC. 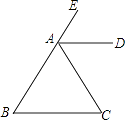
(1)求证:△ABC是等腰三角形.
(2)当∠CAE等于多少度时△ABC是等边三角形?证明你的结论.
【答案】
(1)证明:∵AD平分∠CAE,
∴∠EAD=∠CAD,
∵AD∥BC,
∴∠EAD=∠B,∠CAD=∠C,
∴∠B=∠C,
∴AB=AC.
故△ABC是等腰三角形
(2)解:当∠CAE=120°时△ABC是等边三角形.
∵∠CAE=120°,AD平分∠CAE,
∴∠EAD=∠CAD=60°,
∵AD∥BC,
∴∠EAD=∠B=60°,∠CAD=∠C=60°,
∴∠B=∠C=60°,
∴△ABC是等边三角形
【解析】(1)根据角平分线的定义可得∠EAD=∠CAD,再根据平行线的性质可得∠EAD=∠B,∠CAD=∠C,然后求出∠B=∠C,再根据等角对等边即可得证.(2)根据角平分线的定义可得∠EAD=∠CAD=60°,再根据平行线的性质可得∠EAD=∠B=60°,∠CAD=∠C=60°,然后求出∠B=∠C=60°,即可证得△ABC是等边三角形.
【考点精析】掌握等腰三角形的判定和等边三角形的判定是解答本题的根本,需要知道如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】200粒大米重约4克,如果每人每天浪费1粒米,那么约458万人口的漳州市每天浪费大米用科学记数法表示约为( )
A.9.16×103克B.9.16×104克C.9,16×105克D.0.916×105克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马自驾私家车从A地到B地,驾驶原来的燃油汽车所需的油费108元,驾驶新购买的纯电动汽车所需电费27元.已知行驶1千米,原来燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AD平分∠BAC,AB=AC,连结BD、CD并延长分别交AC、AB于F、E点,则此图中全等三角形的对数为( ) 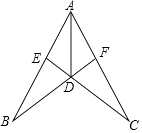
A.2对
B.3对
C.4对
D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com