
【题目】如图,将△ABC绕点C按顺时针旋转60°得到△A′B′C,已知AC=6,BC=4,则线段AB扫过的图形的面积为( )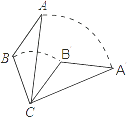
A.![]() π
π
B.![]() π
π
C.6π
D.![]() π
π
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y= ![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).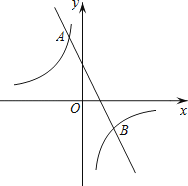
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△MCD平移至△NBA.
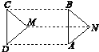
(1)图中平行且相等的线段有____________;
(2)图中相等的角有_______________ (写出三对即可);
(3)能够完全重合的三角形是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是圆0直径BD延长线上的一点,点C在圆0上,AC=BC,AD=CD.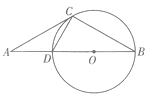
(1)求证:AC是圆0的切线;
(2)若⊙0的半径为2,求 ![]() ABC的面积.
ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图,已知AB∥CD,∠1=∠2,求证:∠3=∠4.
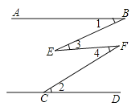
解法展示:证明:延长BE交直线CD于点M,如图所示.
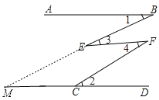
∵AB∥CD,∴∠1=∠BMC(根据1).
∵∠1=∠2,∴∠2=∠BMC(根据2).
∴BE∥CF(根据3).
∴∠3=∠4(根据4).
反思交流:(1)解法展示中的根据1是______________,根据2是______________,根据3是_____________,根据4是____________.
(2)上述命题中,条件记为:①AB∥CD,②∠1=∠2,结论记为:③∠3=∠4.若把其中的一个条件和结论对调,得到一个新命题,写出这个命题(用序号表示即可),判断新命题的真假,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展开后,得折痕AD、BE.(如图①),点O为其交点.如图②,若P、N分别为BE、BC上的动点.如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值=_______.
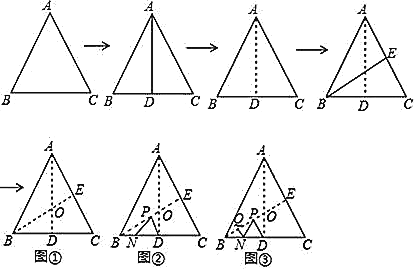
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F,若AF=6,则四边形AEDF的周长是( )
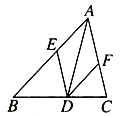
A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com