
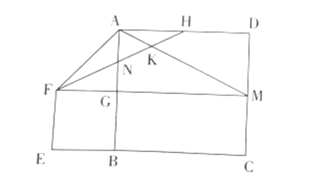
【题目】如图,正方形![]() 的边长为
的边长为![]() ,延长
,延长![]() 至
至![]() 使
使![]() ,以
,以![]() 为边长在上方作正方形
为边长在上方作正方形![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 分别与
分别与![]() 交于点
交于点![]()
![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
A.①②B.①④C.②③D.③④
【答案】B
【解析】
由正方形的性质得到FG=BE=2,∠FGB=90°,AD=4,AH=2,∠BAD=90°,求得∠HAN=∠FGN,AH=FG,根据全等三角形的定理得到△ANH≌△GNF(AAS),故①正确;根据全等三角形的性质得到∠AHN=∠HFG,推出∠AFH≠∠AHF,得到∠AFN≠∠HFG,故②错误;根据矩形的性质得到DM=AG=2,根据三角形的面积公式即可得到![]() ,故③错误;根据全等三角形的性质得到AN=
,故③错误;根据全等三角形的性质得到AN=![]() AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到
AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到![]() ,故④正确.
,故④正确.
解:∵四边形EFGB是正方形,EB=2,∴FG=BE=2,∠FGB=90°,
∵四边形ABCD是正方形,H是AD的中点,∴AD=4,AH=2,∠BAD=90°,
∴∠HAN=∠FGN,AH=FG,
∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠AHN=∠HFG,
∵AG=FG=AH=2,∴AF=![]() FG=
FG=![]() AH,
AH,
∴∠AFH≠∠AHF,
∴∠AFN≠∠HFG,故②错误;
∵延长FG交DC于M,∴四边形ADMG是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,故③错误;
,故③错误;
∵△ANH≌△GNF,∴AN=![]() AG=1,
AG=1,
∵GM=BC=4,∴![]() ,
,
∵∠HAN=∠AGM=90°,∴△AHN∽△GMA,
∴∠AHN=∠AMG,
∵∠AHK=∠HAK,∴AK=HK=NK,故④正确.
故答案选B.


科目:初中数学 来源: 题型:
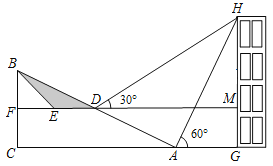
【题目】如图,坡AB的坡度为1:2.4,坡面长26米,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(请将下面两小题的结果都精确到0.1米,参考数据:![]() ≈1.732).
≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)恰为45°,则此时平台DE的长为 米;
(2)坡前有一建筑物GH,小明在D点测得建筑物顶部H的仰角为30°,在坡底A点测得建筑物顶部H的仰角为60°,点B、C、A、G、H在同一平面内,点C、A、G在同一条水平直线上,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业计划购买一些消毒液对厂区内进行消毒,有甲、乙两种型号的消毒液供选择,它们均按瓶销售,每瓶容量都相同.购买甲消毒液![]() 瓶和乙消毒液
瓶和乙消毒液![]() 瓶,需
瓶,需![]() 元;购买
元;购买![]() 瓶甲消毒液与购买
瓶甲消毒液与购买![]() 瓶乙消毒液所需钱数相同.
瓶乙消毒液所需钱数相同.
(1)求甲、乙两种消毒液的单价各是多少元?
(2)现在企业决定只购买甲、乙消毒液中的一种即可,且甲消毒液按原价九折销售,乙消毒液购买![]() 瓶以上超出的部分按原价的六五折销售,设购买
瓶以上超出的部分按原价的六五折销售,设购买![]() 瓶甲消毒液需要
瓶甲消毒液需要![]() 元,购买
元,购买![]() 瓶乙消毒液需要
瓶乙消毒液需要![]() 元,请用分别表示出
元,请用分别表示出![]() 和
和![]() ;
;
(3)在(2)的条件下,已知企业购买消毒液的数量多于![]() 瓶,问购买哪一种消毒液更省钱?
瓶,问购买哪一种消毒液更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
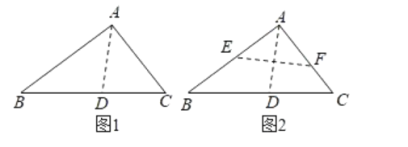
【题目】如图,将直角三角形纸片![]() (
(![]() ,
,![]() )沿过点A的直线折叠,使得AC落在AB边上折痕为AD,展开纸片(如图1);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到
)沿过点A的直线折叠,使得AC落在AB边上折痕为AD,展开纸片(如图1);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到![]() (如图2),若
(如图2),若![]() ,
,![]() ,则折痕EF的长为( )
,则折痕EF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
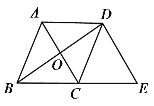
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,AB=5,AC=6,AC的平行线DE交BC的延长线于点E,则四边形ACED的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点四边形ABCD(顶点为网格线的交点).
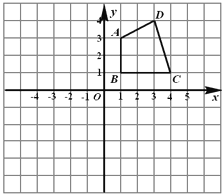
(1)画出四边形ABCD关于x轴成轴对称的四边形A1B1C1D1;
(2)以O为位似中心,在第三象限画出四边形ABCD的位似四边形A2B2C2D2,且位似比为1;
(3)在第一象限内找出格点P,使∠DCP=∠CDP,并写出点P的坐标(写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
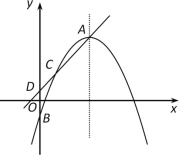
【题目】如图,在平面直角坐标系中,已知二次函数![]() 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
(1)当m=5时,求n的值.
(2)当n=2时,若点A在第一象限内,结合图象,求当y![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
(3)作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com