
科目:初中数学 来源: 题型:
阅读与理解:
(1)先阅读下面的解题过程:
分解因式: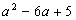
解:方法(1)原式 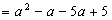 方法(2)原式
方法(2)原式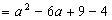
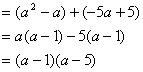
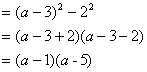
请你参考上面一种解法,对多项式进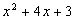 行因式分解.
行因式分解.
(2)阅读下面的解题过程:
已知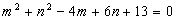 ,试求
,试求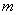 与
与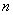 的值.
的值.
解:由已知得: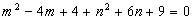
因此得到: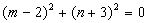
所以只有当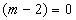 且
且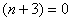 上式才能成立.
上式才能成立.
因而得: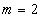 且
且 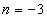
请你参考上面的解题方法解答下面的问题:
已知: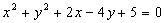 ,试求
,试求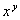 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:线段AB=28cm.
(1)如图1,点P沿线段AB自点A以2cm/秒的速度向点B运动,点P出发2秒后,点Q沿线段BA自点B 以3cm/秒的速度向点A运动,问再经过几秒后P、Q相距4cm?
以3cm/秒的速度向点A运动,问再经过几秒后P、Q相距4cm?

(2)如图2,AO=8cm,PO=4cm,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自点B向点A运动,设点P、Q运动的时间为t(秒).
①当t= 时,∠AOP=90°;
②假若点P、Q两点能相遇,求点Q运动的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
在平行四边形ABCD中,E为CD上一点,DE:EC=1:2,连接AE、BE、BD,且AE、BD交于点F,则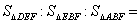 ( )
( )
A.1:3:9 B.1:5:9 C.2:3:5 D.2:3:9
查看答案和解析>>
科目:初中数学 来源: 题型:
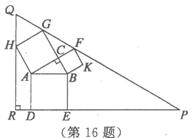 勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB= 4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么APQR的周长等于 .
勾股定理有着悠久的历史,它曾引起很多人的兴趣.l955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB= 4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边_PQ上,那么APQR的周长等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
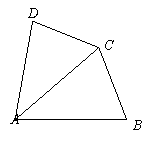
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2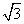 ,P是AC上的一个动点.
,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D、P、B、Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面 积.
积.
查看答案和解析>>
科目:初中数学 来源: 题型:
右图为手的示意图,在各个手指间标记字母A、B、C、D。请你按图中 箭头所指方向(即A®B®C®D®C®B®A®B®C®…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201次出现时,恰好数到
的数是 ;当字母C第2n+1次出现时(n为正整数),恰好数到的数
是 (用含n的代数式表示)。
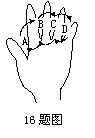 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,A′、E′、B在同一直线上,则∠CBD的度数( )
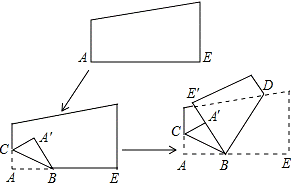
A. 不能确定 B. 大于90° C. 小于90° D. 等于90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com