
”¾ĢāÄæ”涞“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄ“óÖĀĶ¼ĻóČēĶ¼ĖłŹ¾£¬¶„µć×ų±źĪŖ£Ø©2£¬©9a£©£¬ĻĀĮŠ½įĀŪ£ŗ¢Ł4a+2b+c£¾0£»¢Ś5a©b+c=0£»¢ŪČō·½³Ģa£Øx+5£©£Øx©1£©=©1ÓŠĮ½øöøłx1ŗĶx2£¬ĒŅx1£¼x2£¬Ōņ©5£¼x1£¼x2£¼1£»¢ÜČō·½³Ģ|ax2+bx+c|=1ÓŠĖÄøöøł£¬ŌņÕāĖÄøöøłµÄŗĶĪŖ©4£®ĘäÖŠÕżČ·µÄ½įĀŪÓŠ£Ø””””£©
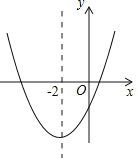
A. 1øö B. 2øö C. 3øö D. 4øö
”¾“š°ø”æB
”¾½āĪö”æøł¾ŻÅ×ĪļĻߵĶ„µć×ų±ź£Ø©2£¬©9a£©£¬øł¾Ż¶„µć×ų±ź¹«Ź½æÉĒóµĆb=4a£¬c=-5a£¬“Ó¶ųæɵĆÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4ax©5a£¬Č»ŗóøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹŅ»Ņ»ÅŠ¶Ļ¼“æÉ£®
”ąa>0£¬
”ßÅ×ĪļĻߵĶ„µć×ų±ź£Ø©2£¬©9a£©£¬
”ą©![]() =©2£¬
=©2£¬![]() =©9a£¬
=©9a£¬
”ąb=4a£¬c=-5a£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4ax©5a£¬
”ą4a+2b+c=4a+8a©5a=7a£¾0£¬¹Ź¢ŁÕżČ·£¬
5a©b+c=5a©4a©5a=©4a£¼0£¬¹Ź¢Ś“ķĪó£¬
”ßÅ×ĪļĻßy=ax2+4ax©5a½»xÖįÓŚ£Ø©5£¬0£©£¬£Ø1£¬0£©£¬
”ąČō·½³Ģa£Øx+5£©£Øx©1£©=©1ÓŠĮ½øöøłx1ŗĶx2£¬ĒŅx1£¼x2£¬Ōņ©5£¼x1£¼x2£¼1£¬ÕżČ·£¬¹Ź¢ŪÕżČ·£¬
Čō·½³Ģ|ax2+bx+c|=1ÓŠĖÄøöøł£¬ŌņÕāĖÄøöøłµÄŗĶĪŖ©8£¬¹Ź¢Ü“ķĪó£¬
¹ŹŃ”B£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijČÕĶõĄĻŹ¦Åå“÷ŌĖ¶ÆŹÖ»·½ųŠŠæģ×߶ĶĮ¶£¬Į½“Ī¶ĶĮ¶ŗóŹż¾ŻČē±ķ£®ÓėµŚŅ»“Ī¶ĶĮ¶Ļą±Č£¬ĶõĄĻŹ¦µŚ¶ž“Ī¶ĶĮ¶²½ŹżŌö³¤µÄ°Ł·ÖĀŹŹĒĘäĘ½¾ł²½³¤¼õÉŁµÄ°Ł·ÖĀŹµÄ3±¶£®ÉčĶõĄĻŹ¦µŚ¶ž“Ī¶ĶĮ¶Ź±Ę½¾ł²½³¤¼õÉŁµÄ°Ł·ÖĀŹĪŖ![]() £®
£®
ĻīÄæ | µŚŅ»“Ī¶ĶĮ¶ | µŚ¶ž“Ī¶ĶĮ¶ |
²½Źż(²½) | 10000 | ____________ |
Ę½¾ł²½³¤(Ć×/²½) | 0.6 | ____________ |
¾ąĄė(Ć×) | 6000 | 7020 |
×¢£ŗ²½Źż”ĮĘ½¾ł²½³¤£½¾ąĄė£®
(1)øł¾ŻĢāŅāĶź³É±ķøńĢīæÕ£»
(2)Ēóx£»
(3)ĶõĄĻŹ¦·¢ĻÖŗĆÓŃÖŠ²½ŹżÅÅĆūµŚŅ»ĪŖ24000²½£¬Ņņ“ĖŌŚĮ½“Ī¶ĶĮ¶½įŹųŗóÓÖ×ßĮĖ500Ć×£¬Ź¹µĆ×ܲ½ŹżĒ”ŗĆĪŖ24000²½£¬ĒóĶõĄĻŹ¦Õā500Ć×µÄĘ½¾ł²½³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB£½90”ć£¬AC£½10cm£¬BC£½5cm£¬µćP“ÓµćC³ö·¢ŃŲĻ߶ĪCAŅŌĆæĆė2cmµÄĖŁ¶ČŌĖ¶Æ£¬Ķ¬Ź±µćQ“ÓµćB³ö·¢ŃŲĻ߶ĪBCŅŌĆæĆė1cmµÄĖŁ¶ČŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£Ø0£¼t£¼5£©£®

£Ø1£©ĢīæÕ£ŗAB£½”” ””cm£»
£Ø2£©tĪŖŗĪÖµŹ±£¬”÷PCQÓė”÷ACBĻąĖĘ£»
£Ø3£©ČēĶ¼2£¬ŅŌPQĪŖŠ±±ßŌŚŅģÓŚµćCµÄŅ»²ą×÷Rt”÷PEQ£¬ĒŅ![]() £¬Į¬½įCE£¬ĒóCE£®£ØÓĆtµÄ“śŹżŹ½±ķŹ¾£©£®
£¬Į¬½įCE£¬ĒóCE£®£ØÓĆtµÄ“śŹżŹ½±ķŹ¾£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć£ŗ£Ø1£©|©3|+£Ø2018©¦Š£©0©![]() +£Ø
+£Ø![]() £©©1
£©©1
£Ø2£©»Æ¼ņ£ŗ£Øa+1£©2©a£Øa©2£©
£Ø3£©½ā·½³Ģ£ŗx2+4x©5=0£»
£Ø4£©2x2©3x©1=0
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶ¼ŠĪ±ä»»ÖŠµÄŹżŃ§£¬ĪŹĢāĒé¾³£ŗŌŚæĪĢĆÉĻ£¬ŠĖȤѧĻ°Š”×é¶ŌŅ»µĄŹżŃ§ĪŹĢā½ųŠŠĮĖÉīČėĢ½¾æ£¬ŌŚRt”÷ABCÖŠ£¬”ĻACB£½90”ć£¬”ĻA£½30”ć£¬µćDŹĒABµÄÖŠµć£¬Į¬½ÓCD£®Ģ½Ė÷·¢ĻÖ£ŗ
£Ø1£©ČēĶ¼¢Ł£¬BCÓėBDµÄŹżĮæ¹ŲĻµŹĒ £»
£Ø2£©ČēĶ¼¢Ł£¬CDÓėABµÄŹżĮæ¹ŲĻµŹĒ £»²¢ĖµĆ÷ĄķÓÉ£®
²ĀĻėŃéÖ¤£ŗ
£Ø3£©ČēĶ¼¢Ś£¬ČōPŹĒĻ߶ĪCBÉĻŅ»¶Æµć£ØµćP²»ÓėµćB£¬CÖŲŗĻ£©£¬Į¬½ÓDP£¬½«Ļ߶ĪDPČʵćDÄꏱÕėŠż×Ŗ60”ć£¬µĆµ½Ļ߶ĪDF£¬Į¬½ÓBF£¬Ēė²ĀĻėBF£¬BP£¬BDČżÕßÖ®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷ÄćµÄ½įĀŪ£»
ĶŲÕ¹ŃÓÉģ£ŗ
£Ø4£©ČōµćPŹĒĻ߶ĪCBŃÓ³¤ĻßÉĻŅ»¶Æµć£¬°“ÕÕ£Ø3£©ÖŠµÄ×÷·Ø£¬ĒėŌŚĶ¼¢ŪÖŠ²¹Č«Ķ¼Ļ󣬲¢Ö±½ÓŠ“³öBF”¢BP”¢BDČżÕßÖ®¼äµÄŹżĮæ¹ŲĻµ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Rt”÷ABCµÄ¶„µćB”¢CµÄ×ų±ź·Ö±šĪŖ(3£¬4)”¢(4£¬2)£¬ĒŅABĘ½ŠŠÓŚxÖį£¬½«Rt”÷ABCĻņ×óĘ½ŅĘ£¬µĆµ½Rt”÷A”äB”äC”䣮ČōµćB”䔢C”äĶ¬Ź±ĀäŌŚŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬ŌņkµÄÖµĪŖ£Ø £©
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬ŌņkµÄÖµĪŖ£Ø £©
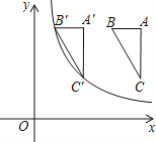
A.2B.4C.6D.8
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
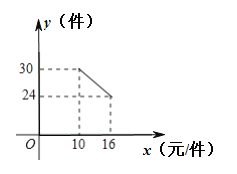
”¾ĢāÄæ”æŅ»ĆūŌŚŠ£“óѧɜĄūÓĆ”°»„ĮŖĶų+”±×ŌÖ÷““Ņµ£¬ĻśŹŪŅ»ÖÖ²śĘ·£¬ÕāÖÖ²śĘ·³É±¾¼Ū10ŌŖ/¼ž£¬ŅŃÖŖĻśŹŪ¼Ū²»µĶÓŚ³É±¾¼Ū£¬ĒŅĪļ¼Ū²æĆŹę¶ØÕāÖÖ²śĘ·µÄĻśŹŪ¼Ū²»øßÓŚ16ŌŖ/¼ž£¬ŹŠ³”µ÷²é·¢ĻÖ£¬øĆ²śĘ·ĆæĢģµÄĻśŹŪĮæy£Ø¼ž£©ÓėĻśŹŪ¼Ūx£ØŌŖ/¼ž£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£Ø1£©ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø2£©ĒóĆæĢģµÄĻśŹŪĄūČóW£ØŌŖ£©ÓėĻśŹŪ¼Ūx£ØŌŖ/¼ž£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öĆ漞ĻśŹŪ¼ŪĪŖ¶ąÉŁŌŖŹ±£¬ĆæĢģµÄĻśŹŪĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æøų³öŅ»øöŹµ¼ŹĪŹĢā£¬Ź¹µĆøł¾ŻĢāŅāĮŠ³öµÄ·½³ĢŹĒ![]() £ŗ______£®
£ŗ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”涫·½¹«Ō°µÄĆÅʱ¼ŪøńČēĻĀ±ķĖłŹ¾£ŗ
¹ŗʱČĖŹż | 1”«50ČĖ | 51”«100ČĖ | 100ČĖŅŌÉĻ |
ĆæČĖĆÅʱ¼Ū | 13ŌŖ | 11ŌŖ | 9ŌŖ |
ijŠ£³õŅ»£Ø1£©£Ø2£©Į½øö°ąČ„ÓĪĄĄ¶«·½¹«Ō°£¬ĘäÖŠ£Ø1£©°ąČĖŹż½ĻÉŁ£¬²»×ć50ČĖ£»£Ø2£©°ąČĖŹż½Ļ¶ą£¬ÓŠ50¶ąČĖ£¬µ«Į½øö°ąŗĻĘšĄ“³¬¹ż100ČĖ. Čē¹ūĮ½øö°ą¶¼ŅŌ°ąĪŖµ„Ī»·Ö±š¹ŗʱ£¬ŌņŅ»¹²Ó¦ø¶1240ŌŖ£»Čē¹ūĮ½øö°ąĮŖŗĻĘšĄ“£¬×÷ĪŖŅ»øöĶÅĢå¹ŗʱ£¬ŌņÖ»Ščø¶936ŌŖ.
£Ø1£©ĮŠ·½³Ģ»ņ·½³Ģ×éĒó³öĮ½øö°ąø÷ÓŠ¶ąÉŁŃ§Éś£æ
£Ø2£©Čē¹ūĮ½øö°ą²»ĮŖŗĻĀņʱ£¬ŹĒ²»ŹĒ³õŅ»£Ø1£©°ąµÄѧɜ·ĒŅŖĀņ13ŌŖµÄʱÄŲ£æÄćÓŠŹ²Ć“Ź”Ē®·½Ź½Ą“°ļĖūĆĒĀņʱÄŲ£æĖµĖµÄćµÄĄķÓÉ.
£Ø3£©ÄćČĻĪŖŹĒ·ń“ęŌŚÕāŃłµÄæÉÄÜ£ŗ51”«100ČĖÖ®¼äĀņʱµÄĒ®ŹżÓė100ČĖŅŌÉĻĀņʱµÄĒ®ŹżĻąµČ£æČē¹ūÓŠ£¬ŹĒ¶ąÉŁČĖÓė¶ąÉŁČĖĀņʱĒ®ŹżĻąµČ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com