
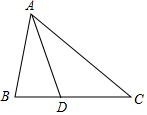
 如图,在△ABC中,AD平分∠BAC.
如图,在△ABC中,AD平分∠BAC.分析 (1)过D作DE⊥AB于E,DF⊥AC于F,根据角平分线的性质得到DE=DF,根据三角形的面积公式即可得到结论;
(2)根据三角形角平分线定理即可得到结论.
解答  (1)证明:过D作DE⊥AB于E,DF⊥AC于F,
(1)证明:过D作DE⊥AB于E,DF⊥AC于F,
∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=$\frac{1}{2}$AB•DE,S△ACD=$\frac{1}{2}$AC•DF,
∴S△ABD:S△ACD=($\frac{1}{2}$AB•DE):($\frac{1}{2}$AC•DF)=AB:AC;
(2)解:∵AD平分∠BAC,
∴$\frac{AB}{AC}=\frac{BD}{CD}$=$\frac{4}{5}$,
∴BD=$\frac{4}{5}$CD,
∵BC=6,
∴BD=$\frac{8}{3}$.
点评 本题考查了三角形的角平分线的性质,三角形角平分线定理,三角形的面积公式,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
 如图,有一正方形桌面ABCD,一顶点B在水平地面上,其中两顶点A、C到地面的距离分别是0.5m和1m,则桌面的边长为$\frac{1}{2}$$\sqrt{5}$m.
如图,有一正方形桌面ABCD,一顶点B在水平地面上,其中两顶点A、C到地面的距离分别是0.5m和1m,则桌面的边长为$\frac{1}{2}$$\sqrt{5}$m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
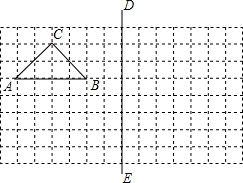 如图,在所给网格图(每小格均为边长是1的正方形)中完成下各题:(用直尺画图)
如图,在所给网格图(每小格均为边长是1的正方形)中完成下各题:(用直尺画图)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
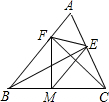 如图在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是( )
如图在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=3,BC=8,则△EFM的周长是( )| A. | 21 | B. | 15 | C. | 13 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com