练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

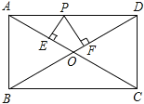
    【题目】如图，矩形ABCD的两边AB=3，BC=4，P是AD上任一点，PE⊥AC于点E，PF⊥BD于点F.求PE+PF的值.

    【答案】

    【解析】

    首先连接OP．由矩形ABCD的两边AB=3，BC=4，可求得OA=OD=，S△AOD=S矩形ABCD然后由S△AOD=S△AOP+S△DOP=OAPE+ODPF=OA（PE+PF）=×（PE+PF）=3，求得答案．

    解：连接OP，
    ∵矩形ABCD的两边AB=3，BC=4，
    ∴S矩形ABCD=ABBC=12，OA=OC，OB=OD，AC=BD，AC==5，
    ∴S△AOD=S矩形ABCD=3，OA=OD=，

    ∵PE⊥AC， PF⊥BD
    ∴S△AOD=S△AOP+S△DOP=OAPE+ODPF=OA（PE+PF）=×（PE+PF）=3，
    ∴PE+PF=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平行四边形ABCD中，分别以AD、BC为边向内作等边△ADE和等边△BCF，连接BE、DF．求证：四边形BEDF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，∠ACB＝90°点E是AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE，求证四边形ACEF是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法正确的有（ ）

    ①不相交的两条直线是平行线；

    ②经过直线外一点，有且只有一条直线与这条直线平行；

    ③两条直线被第三条直线所截，同旁内角互补；

    ④在同一平面内，若直线，则直线与平行．

    A.个B.个C.个D.个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x、y的方程组 （a≥0），给出下列说法：
    ①当a=1时，方程组的解也是方程x+y=2的一个解；
    ②当x﹣2y＞8时，a＞ ；
    ③不论a取什么实数，2x+y的值始终不变；
    ④某直角三角形的两条直角边长分别为x+y，x﹣y，则其面积最大值为 ．
    以上说法正确的是（ ）
    A.②③
    B.①②④
    C.③④
    D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

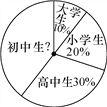
    【题目】某次学生夏令营活动，有小学生、初中生、高中生和大学生参加，共200人，各类学生人数比例见扇形统计图．

    (1)参加这次夏令营活动的初中生共有多少人？

    (2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款．结果小学生每人

    捐款 5 元，初中生每人捐款 10 元，高中生每人捐款 15 元，大学生每人捐款 20 元．问平均 每人捐款是多少元？

    (3)在(2)的条件下，把每个学生的捐款数额(以元为单位)——记录下来，则在这组数据中，众数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分、80分、90分、100分，并根据统计数据绘制了如下不完整的统计图表：

    乙校成绩统计表

    分数/分

    人数/人

    70

    7

    80

    90

    1

    100

    8

    (1)在图①中，“80分”所在扇形的圆心角度数为________；

    (2)请你将图②补充完整；

    (3)求乙校成绩的平均分；

    (4)经计算知s甲2＝135，s乙2＝175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，∠C＝60°，D，E分别是边AB，BC上两点，且DE∥AC，下列结论不正确的是( )

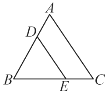
    A. ∠A＝60° B. △BDE是等腰三角形 C. BD≠DE D. △BDE是等边三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①、②、③，正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形，点M、N分别从点B，C开始，以相同的速度中⊙O上逆时针运动．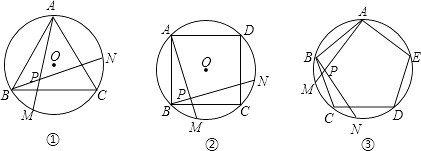

    （1）求图①中∠APB的度数；
    （2）图②中，∠APB的度数是 ， 图③中∠APB的度数是；
    （3）根据前面探索，你能否将本题推广到一般的正n边形情况？若能，写出推广问题和结论；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案