练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．当k为何值时，关于x的方程3x-2k=4（x-k）+1的解是非正数？

    分析 解关于x的方程求得x=2k-1，根据解为非正数得出不等式，解之可得．

    解答 解：解方程3x-2k=4（x-k）+1，得：x=2k-1，
    由题意得2k-1≤0，
    解得：k≤$\frac{1}{2}$．

    点评 本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届湖北省大冶市九年级3月月考数学试卷（解析版） 题型：单选题

    如图是二次函数y=ax2+bx+c的图象，下列结论：

    ①二次三项式ax2+bx+c的最大值为4；

    ②4a+2b+c＜0；

    ③一元二次方程ax2+bx+c=1的两根之和为﹣1；

    ④使y≤3成立的x的取值范围是x≥0．其中正确的个数有（　　）

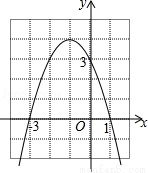
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源：2017届广西马山县民族中学春季学期第一次月考八年级数学试卷（解析版） 题型：填空题

    计算=____________________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知函数y=（n+3）x|n|-2是关于x的一次函数，则n=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．在一次函数y=（2-k）x中，y随x的增大而增大，则k的取值范围为k＜2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知反比例函数y=$\frac{-k}{x}$（k≠0）的图象上有点A（1，-k）和B（-1，k），点C（-$\frac{1}{2}$，n）在直线y=k（x+$\frac{7}{4}$）上，
    且AC=5BC，求当y＜2时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，正方形ABCD中，点E是AB边上一动点（点E与点B不重合），点E到达点A时运动停止，点F是射线BC上一点．且∠EFB=30°，设BE=x，△BEF与正方形ABCD重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤m，m＜x≤3时．函数的解析式不同）．
    （1）填空：正方形ABCD的边长为3，图2中b的值为$\frac{3}{2}\sqrt{3}$；
    （2）求S关于x的函数关系式，并写出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．某地区为了进一步缓解交通拥堵问题，决定修建一条长为6千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）之间在50≤x≤120时，具有一次函数的关系，如表所示．
    x5080100120
    y40343026
    （1）求y关于x的函数解析式；
    （2）如果修建70天，那么平均每天的修建费是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

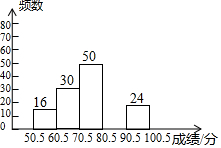    2．某校组织1000名学生参加“青少年普法知识大赛”，为了了解学生的参赛成绩，从中抽取部分学生的参赛成绩（成绩均为整数）进行统计，并绘制成如下的不完全统计图表．
    组别分数段频数频率
    一50.5-60.5160.08
    二60.5-70.5300.15
    三70.5-80.5500.25
    四80.5-90.5m0.40
    五90.5-100.524n
    请根据所给信息，解答下列问题：
    （1）表中m=80，n=0.12；
    （2）补全频数分布直方图；
    （3）若成绩超过80分为优秀，分别求出被抽取的学生中优秀的学生频数和频率．

    查看答案和解析>>

    同步练习册答案