
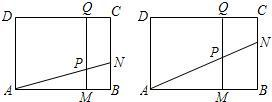
 N的面积都相等?若存在,求a的值;若不存在,请说明理由.
N的面积都相等?若存在,求a的值;若不存在,请说明理由. | NB |
| AD |
| PN |
| PA |
| PN |
| PA |
| BM |
| AM |
| NB |
| AD |
| BM |
| AM |
| PM |
| NB |
| AM |
| AB |
| 3 |
| 4 |
| NB |
| AD |
| PN |
| PA |
| PN |
| PA |
| BM |
| AM |
| NB |
| AD |
| BM |
| AM |
| PM |
| BN |
| AM |
| AB |
| PM |
| t |
| a-t |
| a |
| t(a-t) |
| a |
| t(a-t) |
| a |
| (QP+AD)DQ |
| 2 |
| (MP+BN)BM |
| 2 |
(3-
| ||
| 2 |
(
| ||
| 2 |
| 6a |
| 6+a |
| 6a |
| 6+a |
| t |
| a |
| 6a |
| 6+a |
| 3 |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
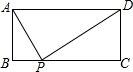 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com