
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

【答案】答案不唯一(例:先将△ABC以点B为旋转中心顺时针旋转90,再将得到的图形向右平移2个单位向下平移2个单位即可)
【解析】
根据“平移”、“轴对称”和“旋转”的性质进行分析解答即可.
根据题意,可按下列方式变换使点A与点E重合,点B与点D重合:
(1)先将△ABC以点B为旋转中心顺时针旋转90,再将得到的图形向右平移2个单位,并向下平移2个单位即可;
(2)先将△ABC向右平移2个单位,再向下平移2个单位,然后将所得△ABC绕点B顺时针旋转90°即可;
……
故答案为:本题答案不唯一,如:先将△ABC以点B为旋转中心顺时针旋转90,再将得到的图形向右平移2个单位向下平移2个单位即可.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示
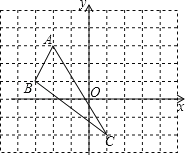
(1)请画出△ABC关于y轴对称的△A′B′C′;(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′B′C′三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
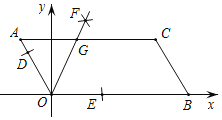
A. (![]() ﹣1,2) B. (
﹣1,2) B. (![]() ,2) C. (3﹣
,2) C. (3﹣![]() ,2) D. (
,2) D. (![]() ﹣2,2)
﹣2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)求点B的坐标.
(2)将平行四边形OABC向左平移![]() 个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
(3)求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 分别为定角( 大小不会发生改变)
分别为定角( 大小不会发生改变) ![]() 内部的两条动射线,
内部的两条动射线,

(1)当![]() 运动到如图1的位置时,
运动到如图1的位置时,![]() ,求
,求![]() 的度数.
的度数.
(2)在(1)的条件下(图2),射线![]() 分别为
分别为![]() 的平分线,求
的平分线,求![]() 的度数.
的度数.
(3)在(1)的条件下(图3),![]() 是
是![]() 外部的两条射线,
外部的两条射线,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,在射线AN上取一点B,使
,在射线AN上取一点B,使![]() ,过点
,过点![]() 作
作![]() 于点C,点D是线段AB上的一个动点,E是BC边上一点,且
于点C,点D是线段AB上的一个动点,E是BC边上一点,且![]() ,设AD=x cm,BE=y cm,探究函数y随自变量x的变化而变化的规律.
,设AD=x cm,BE=y cm,探究函数y随自变量x的变化而变化的规律.

(1)取指定点作图.根据下面表格预填结果,先通过作图确定AD=2cm时,点E的位置,测量BE的长度。
①根据题意,在答题卡上补全图形;
②把表格补充完整:通过取点、画图、测量,得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
|
|
| 2 | 3 |
|
|
|
| 2.9 | 3.4 | 3.3 | 2.6 | 1.6 | 0 |
(说明:补全表格时相关数值保留一位小数)
③建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(2)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的取值约为__________
的取值约为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水果市场某品种苹果的销售方式如下表:
购买苹数量(千克) | 不超过 | 超过 |
每千克的价格(元) |
|
|
(1)如果小明购买![]() 千克的苹果,那么他需要付___________元.
千克的苹果,那么他需要付___________元.
(2)小明分两次共购买![]() 千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付
千克的苹果,第二次购买的数量多于第一次购买的数量,若他两次共付![]() 元,求他两次分别购买苹果的数量.
元,求他两次分别购买苹果的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
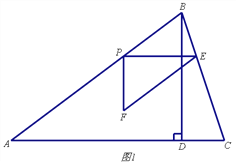
【题目】如图1,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)
(t>0).
(1)求线段AC的长.
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式,并写出t的取值范围.
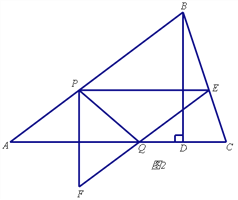
(3)若边EF所在直线与边AC交于点Q,连结PQ,如图2,直接写出△ABC的某一顶点到P、Q两点距离相等时t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com